Physicists have released the most accurate measurement yet of the expansion of the universe. The unexpected results suggest that the rate of expansion is faster than the prediction based on the physics of the early universe. Ultimately, this discrepancy means that we might be missing an important piece of the grand puzzle of how the universe works.
Faster acceleration or just not enough physics?
Cosmologists characterize the universe’s expansion in a simple law known as Hubble’s Law, named after Edwin Hubble, who first observed that the universe is in constant expansion after studying the Doppler shift of retreating nebulae. Hubble’s Law is the observation that more distant galaxies are moving away at a faster rate, meaning galaxies that are close by are moving away relatively slowly by comparison. The relationship between the speed and the distance of a galaxy is set by “Hubble’s Constant”, which essentially indicates the rate of expansion of the universe.
The history of the measurement of Hubble’s Constant has been always fraught with challenges and unexpected revelations. In 1929, Hubble thought that the value must be about 550,395 kilometers (342,000 miles) per hour per million light years – about ten times larger than what we measure now. But with each major discrepancy, physics became richer. It’s thanks to more precise measurements of Hubble’s constant over the years that actually led to the inadvertent discovery of dark energy, a mysterious type of energy which we cannot directly detect but which physicists are confident makes up at least 70% of the energy of the universe.
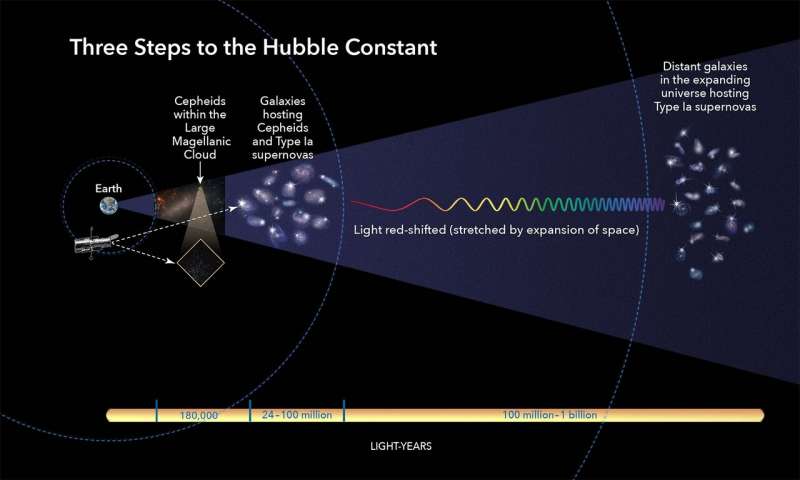
Nowadays, astronomers’ calculations of the Hubble’s Constant rely on something called ‘standard candles’ — stellar objects that give a certain, known amount of light — also called Cepheid variable stars. A study released last year based on Cepheid variable star data suggested that the rate of expansion is 73.5 kilometers (45.6 miles) per second per megaparsec. Meanwhile, we have the very precise measurements of the Cosmic Microwave Background – the afterglow of the Big Bang – from the Planck mission, which has measured the Hubble Constant to be about 74,350 kilometers (46,200 miles) per hour per million light-years or 67.4 km/s/Mpc.

More recently, a team of researchers led by Adam Riess, a professor of physics and astronomy at The Johns Hopkins University in Baltimore and a laureate of the 2011 Nobel Prize for physics, found an even higher rate for the Hubble Constant. Using a new method, the research team studied 70 Cepheid variables in the Large Magellanic Cloud, arriving at a Hubble Constant of 74.03 ks/s/Mpc. That’s about 9% faster than the “expected” value derived from the Planck data. According to the astronomers, the chance that these results are somewhat mistaken is about one in 100,000.
“This mismatch has been growing and has now reached a point that is really impossible to dismiss as a fluke,” Riess said in a statement. “This is not what we expected.”
“This is not just two experiments disagreeing. We are measuring something fundamentally different,” he added.
“One is a measurement of how fast the universe is expanding today, as we see it. The other is a prediction based on the physics of the early universe and on measurements of how fast it ought to be expanding,” he added. “If these values don’t agree, there becomes a very strong likelihood that we’re missing something in the cosmological model that connects the two eras.”
These new results suggest that our current understanding of physics is inadequate and that something important is missing. One possible explanation might be that the acceleration might be due to an increase in the density of dark energy. An alternative explanation might be that dark matter interacts more strongly with ordinary matter than previously thought. A less exciting explanation could be that there are “unknown unknowns” in the data caused by systematic effects and that a more careful analysis may one day reveal a subtle effect that has been overlooked.
The findings appeared in The Astrophysical Journal.