
Here’s a problem which sounds simple enough, but isn’t: find three numbers so that the sum of their cubes is equal to 42. A planetary scientist just solved the problem, and the numbers will definitely surprise you.
The original problem was laid out in 1954 at the University of Cambridge, and was very straightforward: find the solutions for x3+y3+z3=k, with k being all the numbers from one to 100. Some of them are pretty obvious. Just take 1, 2, and 3, sum their cubes, and you end up with 1+8+27=36 — so you have an answer to 36. You can be a bit clever and use -1 instead of 1, which leaves you with -1+8+27=34, and you have another solution. After you take out all these easy solutions, you’re left with some weird ones though.
There should be a solution for all numbers, but two proved particularly different to crack: 33 and 42. Thanks to a creative approach (and a week at a world-leading supercomputer), Professor Andrew Booker managed to solve it for 33. Coincidence or not, the only remaining number was 42 — which fans of the Hitchhiker’s Guide to the Galaxy will recognize as “the answer to Everything”, according to a fictional computing machine that worked for 7 million years.
Booker tried to solve the equation for 42, but couldn’t — so he turned to MIT maths professor Andrew Sutherland. Together, the two used a machine that’s surprisingly similar to the fictional one described above. The platform is called Charity Engine: a ‘worldwide computer’ that harnesses idle, unused computing power from over 500,000 home PCs to create a crowd-sourced, super-green platform made entirely from otherwise wasted capacity. It didn’t take 7 million years, but it did take quite a long time. Yet, at the end of it all, the two had their answer.
Are you ready?
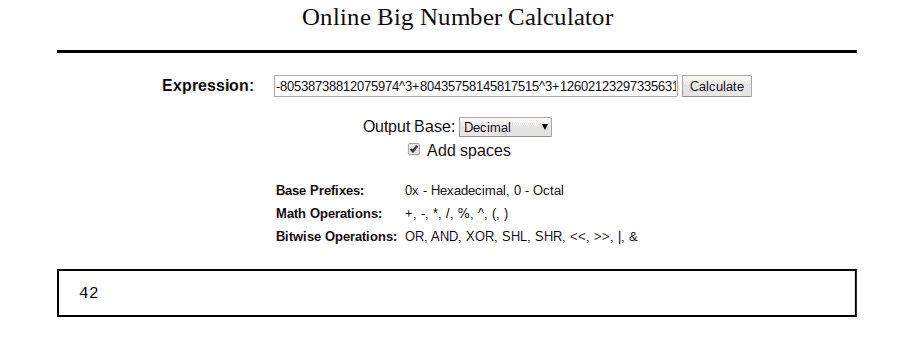
The three numbers for which the sum of their cubes is equal to 42 are:
- X = -80538738812075974
- Y = 80435758145817515
- Z = 12602123297335631
These three incredibly large numbers are the solution to the problem — trust us, we did the math.
But while doing the math is easy if you have a big calculator, it’s not easy to reach these numbers in the first place. These 17-digit monsters are so big that brute-forcing calculations just won’t work. Instead, researchers used clever algorithms to help finesse the search. But there was no guarantee if or when they would find the solution. Booker, who is based at the University of Bristol’s School of Mathematics, says he’s glad the search is finally over:
“I feel relieved. In this game it’s impossible to be sure that you’ll find something. It’s a bit like trying to predict earthquakes, in that we have only rough probabilities to go by. So, we might find what we’re looking for with a few months of searching, or it might be that the solution isn’t found for another century.”
With ingenuity and sufficient computing power, you can solve almost any problem. Who knows, one day we might even learn the answer to Everthing — and it might be 42.






