Japanese researchers have described one of nature’s most ubiquitous patterns: a model which accurately describes how leaves grow on plants.
“We developed the new model to explain one peculiar leaf arrangement pattern. But in fact, it more accurately reflects not only the nature of one specific plant, but the range of diversity of almost all leaf arrangement patterns observed in nature,” said Associate Professor Munetaka Sugiyama from the University of Tokyo’s Koishikawa Botanical Garden.
Plant leaves have fascinated mankind since time immemorial. Some, like the sunflower, grow in a remarkably ordered geometry. Others seem to be much more chaotic, not subject to any apparent rule. There’s even a special name to describe the growth pattern of leaves on a plant: phyllotaxis.
Understandably, mathematicians have also been fascinated with these patterns. Leonardo da Vinci made observations of the spiral arrangements of plants, although he did not leave behind too many comments. Later on, naturalists noted that the spiral phyllotaxis of plants was sometimes clockwise and otherwise anti-clockwise, but it seemed to follow the so-called mathematical golden ratio.
It became clear that many plants follow a mathematical distribution, but no one was able to find a universal law to describe leaf growth.
In 1996, though, researchers got really close. Douady and Couder developed an algorithm that could account for many, but not all leaf arrangement patterns. This became known as the DC2 equation, and to this day, it is used to infer different variables of plant physiology.
Now, Japanese researchers believe they have found an even better rule, which can account for all the patterns in plants.
Unruly exceptions
They started out from a group of plants called “orixate”, from the species Orixa japonica, a shrub native to Japan, China, and the Korean peninsula. Orixate plants are part of an unruly group that doesn’t obey the DC2 equation. The angles between O. Japonica leaves are 180 degrees, 90 degrees, 180 degrees, 270 degrees, and then the next leaf resets the pattern to 180 degrees.
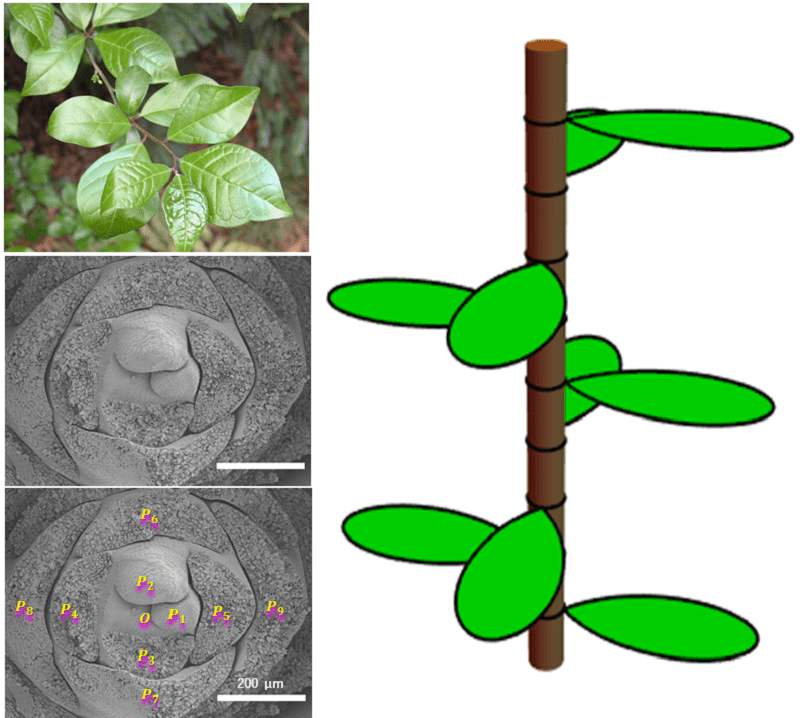
At least four other unrelated plants groups follow a similar pattern. Sugiyama and colleagues wanted to see if they could find another equation to describe these plants, starting from the fundamental genetic and cellular machinery shared by all plants. The reason they took this approach is that if four separate groups all evolved this pattern, then it seems likely that there’s an underlying reason for it. Having it randomly pop up 4 times is just too unlikely.
They started from the two main shortcomings of the DC2 equation:
- No matter what parameters you put into it, some leaf arrangements are just not accounted for.
- The Fibonacci spiral leaf arrangement pattern is the most common spiral pattern observed in nature but is only modestly more common than other spiral patterns calculated by the DC2 equation.
To address these, the team focused on one key assumption of the equation: that leaves emit a constant signal to inhibit the growth of other nearby leaves. This makes sense because the plant would want some balance, and there is some research suggesting that this signal is propagated through a hormone called auxin, although the exact mechanism is not yet clear.
Sugiyama did away with the assumption that this signal was constant.
“We changed this one fundamental assumption – inhibitory power is not constant, but in fact changes with age. We tested both increasing and decreasing inhibitory power with greater age and saw that the peculiar orixate pattern was calculated when older leaves had a stronger inhibitory effect,” said Sugiyama. In other words, the older a leaf is, the less likely it is for new leaves to grow in its direct vicinity.
The resulting equation was not only capable of explaining the growth pattern of orixate plants but fit much better with the pattern observed in all plants, researchers claim.
“Our research has the potential to truly understand beautiful patterns in nature,” said Sugiyama.
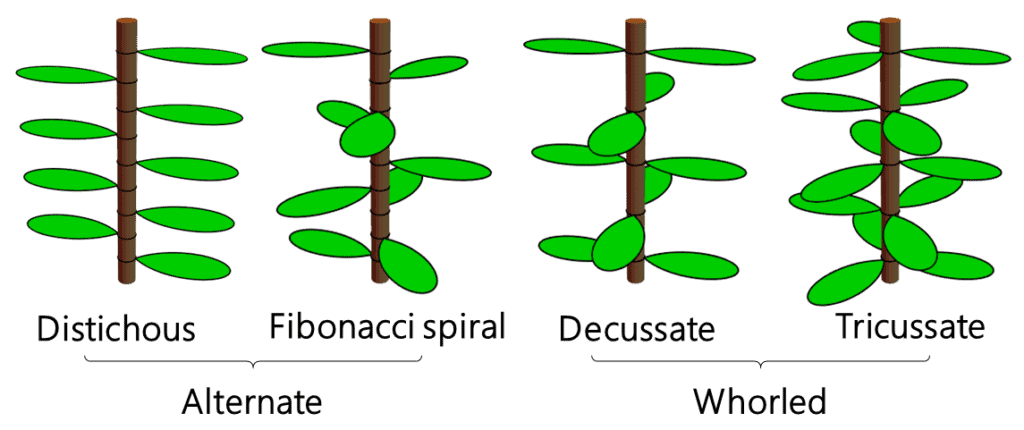
However, there are still some shortcomings with this model — while it did account for most of the exceptions, it didn’t account for all the exceptions.
“There are other very unusual leaf arrangement patterns that are still not explained by our new formula. We are now trying to design a new concept that can explain all known patterns of leaf arrangement, not just almost all patterns,” said Sugiyama.
It remains to be seen if biologists or other researchers working with this equation will confirm its results and incorporate it into their work. For now, the relationship between mathematics and botany seems to have gotten even deeper.
Journal Reference: Takaaki Yonekura, Akitoshi Iwamoto, Hironori Fujita, Munetaka Sugiyama. 2019. Mathematical model studies of the comprehensive generation of major and minor phyllotactic patterns in plants with a predominant focus on orixate phyllotaxis. PLOS Computational Biology. DOI: 10.1371/journal.pcbi.1007044.







