The funny thing about math is that it offers answers to questions you didn’t even think of asking. For instance, did you know that there are 15, and only 15 ways of covering a floor with pentagonal tiles?

Tiling a plane with a single pattern has fascinated people since the Antiquity, not only for the sake of geometry but also for aesthetic reasons. That’s how mosaics got started, and how they became the way to exhibit opulence and social status. Most mosaics were covered with rectangular or square tiles. It didn’t take long for the ancients to understand that a floor can also be tiled with triangles or hexagons, and that was pretty much the end of it, until much later.
This characteristic of a shape, the ability to cover an endless plane pattern, is called tessellation. In 1918, Karl Reinhardt published a thesis on tessellation in which he carried out an exhaustive search for all the convex forms (all angles smaller than 180°) that can tile a plane without overlapping. He showed that all types of triangles and four-sided shapes can tile a plane, and only three types of hexagons can do so. He also showed that no polygon with seven or more sides could do so.
The only question mark that remained was that of pentagons.
Now, almost a hundred years later, that pressing question has been answered by Michaël Rao of the Laboratoire d’informatique du parallélisme (CNRS/Inria/ENS de Lyon/Université Claude Bernard Lyon 1).
Five sides
So far, we know of 15 types of pentagons which could fill the tile — many described by Reinhardt himself, several identified by other mathematicians, even amateurs. In 2015, the 15th type was described, 30 years after the previous. But there was no definitive answer as to whether others also remained. In a rather witty introductory note, Reinhardt said his thesis didn’t demonstrate that the list is exhaustive “for the excellent reason that a complete proof would require a rather large book.”
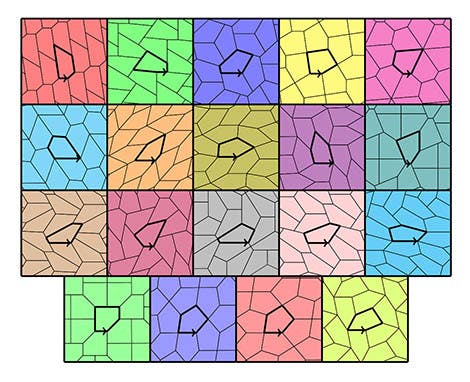
Rao started with a computer algorithm which generated all possible pentagonal shapes. In his new computer-assisted proof, he used a computer algorithm and found a total of 371 families of pentagons. They were defined by a common rule, such as “side A is equal to side B” or “Angle C and D are equal.”
“For each of the 371 scenarios,” explainedGreg Kuperberg, a professor of mathematics at the University of California, Davis., “his algorithm tries to piece together a tiling by laying down one tile at a time, using only the allowed vertex configurations.
Here’s a visualization of the computer algorithm:
A video of Rao’s computer program running through tiling possibilities and arriving at the 15th type of pentagon tiling.
Out of these, only 19 were convex and could successfully tile a plane. As it turned out, four of these are particular cases of these 15 types, so lo and behold, 15 and only 15 types of pentagons can fill a tile.
Seeking einstein
Thomas Hales, a professor of mathematics at the University of Pittsburgh and a leader in using computer programming to solve problems in geometry, has independently replicated Rao’s solutions. Rao’s study also provides insight into the search of the legendary einstein (no relation to Albert Einstein, the word just means “one rock” in German). The einstein is a hypothetical shape that can only tile the plane nonperiodically, in a never-repeating orientation pattern. “For everybody who works on tiling, this is a kind of holy grail,” Rao said referring to the einstein. He sees this study not as a goal in itself, but rather as a milestone in a much larger quest.
There’s good reason to believe that at least an einstein exists though if it does, it likely has a very complex shape. As you can imagine, this only adds to its allure.
Researchers believe that the einstein exists because it connects to another problem in tiling theory, called the decision problem. Casey Mann, an associate professor of mathematics at the University of Washington who discovered the 15th tessellating pentagon describes the decision problem:
“The question is, if someone hands you a tile, can you come up with a computer algorithm that will take as input that tile and say, ‘Yes, this tiles the plane,’ or, ‘No, it doesn’t?’”
“Most people think there’s too much complexity for such an algorithm to exist,” Mann said.
But Rao plans to move on and set his algorithms on the search for the elusive einstein. Who knew there was so much complexity to tiling, eh?
Journal Reference: Exhaustive search of convex pentagons which tile the plane. Michaël Rao, available on Arxiv.org, arXiv:1708.00274
Bonus question
Can you figure out why a floor can’t be tiled with heptagonal shapes? It’s a fairly two-liner simple mathematical proof. Hint: the sum of the heptagon’s interior angles is 900 degrees.
Was this helpful?



