Both bathroom decorators and mathematicians have a reason to rejoice (how often does that happen?). Using a computer algorithm, a group of mathematicians at the University of Washington Bothell discovered the 15th kind of pentagon that can tile in a plane. The 14th was discovered in 1985 by mathematician Rolf Stein, while the previous five before were proven by Majorie Rice, a housewife from San Diego.

You can’t tile a regular pentagon – with all its sides and interior angles equal – but you can tile triangles and squares in innumerable shapes and sizes. As for a convex heptagon or octagon, it was mathematically proven there’s no such shape that can tile in a plane. Tiling pentagons, however, is an open problem, one that’s been fascinating mathematicians for over a century. The first to prove a pentagon could be tiled was German mathematician Karl Reinhardt who discovered five such shapes that tile in 1918.

For almost thirty years there was no tiling pentagon reported, but now using the power of computing Casey Mann, Jennifer McLoud and David Von Derau of the University of Washington Bothell have finally found a new one.
“The problem of classifying convex pentagons that tile the plane is a beautiful mathematical problem that is simple enough to state so that children can understand it, yet the solution to the problem has eluded us for over 100 years,” said Casey for the Guardian. “The problem also has a rich history, connecting back to the 18th of David Hilbert’s famous 23 problems.”
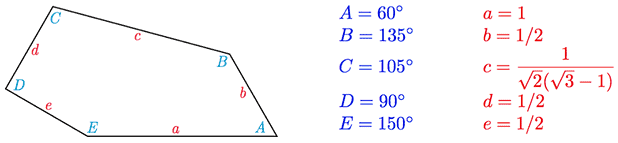
To find the tiling pentagon, the researchers basically used brute force to search a large, but finite set of possibilities. Eventually they got lucky, but are there more? It’s a simple, yet challenging problem at the same time. After all, it took a 30 years dry spell.
Of course, there are practical uses to finding tiling surfaces, from biochemistry to structural design.
“Many structures that we see in nature, from crystals to viruses, are comprised of building blocks that are forced by geometry and other dynamics to fit together to form the larger scale structure,” he added.
“I am too cautious to make predictions about whether or not more pentagon types will be found, but we have found no evidence preventing more from being found and are hopeful that we will see a few more. As we continue our computerized enumerations, we also hope to gather enough data to start making specific predictions that can be tested.”







