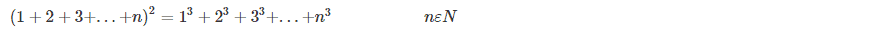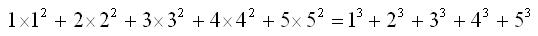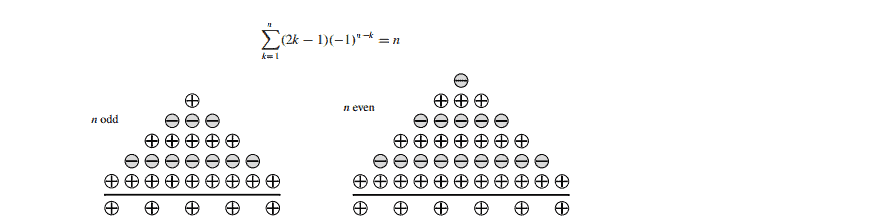“Beauty is the first test; there is no permanent place in the world for ugly mathematics,” G. H. Hardy (1877-1947)
One study that looked at the brain patterns of 15 mathematicians while they reacted to seeing a beautiful equation found it had the same response as magnificent art or music. Ask mathematicians what makes their trade beautiful and you’ll end up with some mixed answers. Some will agree, however, that symmetry, proportion and elegance play a part. I would also add simplicity and to illustrate, here are a couple I’ve always found entertaining.
Pythagorean Theorem
Quite possible the most famous theorem in mathematics, Pythagoras’ Theorem states that square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. Whether Pythagoras (c.560-c.480 B.C.) or someone else from his School was the first to discover its proof can’t be claimed with any degree of credibility. Euclid’s (c 300 B.C.) Elements is considered the first proof of the theorem, but far from being the only one. There are at least 114 approaches to proving the theorem. Mathematician Bhaskara (about 1114-1185) proved the Pythagorean Theorem simply by drawing this picture and saying “Behold!”
Confused? Check out this explanation.
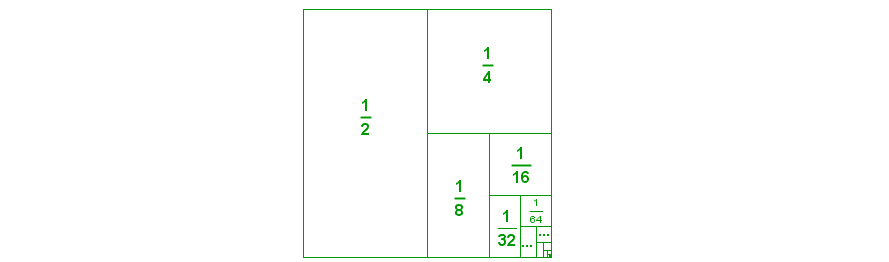
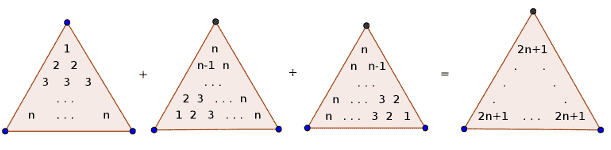
Simple number series
This might not exactly constitute a proof, but a great visual representation nonetheless.
And a joke to complement. An infinite number of mathematicians walk into a bar. The first one orders a beer. The second one orders half a beer. The third one orders a quarter of a beer. The bartender stops them, pours two beers and says, “You’re all a bunch of idiots.”
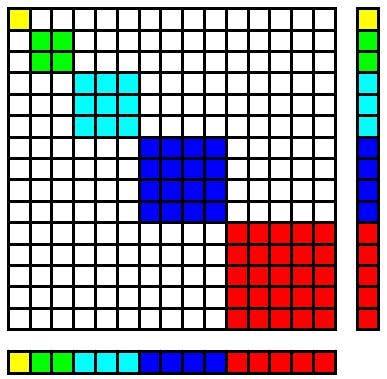
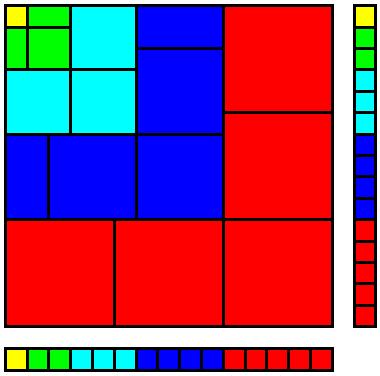
Adding cubes
In number theory, there is a curious relationship between the sum of consecutive cubes of the set of natural numbers and the square of the sum of the corresponding numbers themselves. A visual representation of this solution might seem to entail a volume problem, but this great solution uses only an area model.
This is a simple 15 by 15 square, where each number from 1 to 5 is colour coded on each side of the square. Obviously, the area of the square is 1 + 2 + 3 + 4 + 5 times 1 + 2 + 3 + 4 + 5 (left hand side of the equation). The unaccounted small squares can be arranged again into new squares, where the two rectangles can rearranged into squares.
Thus we get the whole equation as follows:
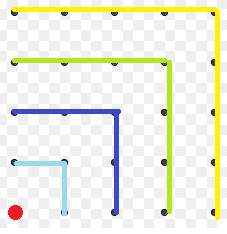
Dots and lines
Consider the following array of points.
We’ll use it the following equation:
How so? Well, let’s see what happens if we connect the dots with lines.
Since it’s the first point, there is no line to connect the first red dot. The second blue line has three points connecting the segments; the purples one has five points; and so on until the last line has 2n−1 points on it.
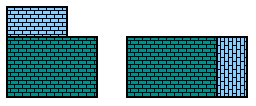
The 1 + 2 + 3 + 4 + · · · infinite series
Just like in the “adding cubes” example, we again draw a grid. This time a rectangle with one side’s length n and the other n+1.
The area of the entire rectangle is n*(n+1), but since only half of it colored (the sum) we can immediately and intuitively say that the sum is half the area, hence n(n+1)/2.
x2 – y2 = (x+y) (x-y)
At left is a large square (of side length x) with a small square (of side length y) cut out of the corner. (Thus its total area is x2 – y2).
After making the subtraction, we can identify two rectangles which we’ll assign each a colour. By rearranging the two rectangles two form one uniform rectangle, then we can write its area as follows: (x-y) [one side] times (x+y) [the other side].
Alternating sum of odd numbers
The cube
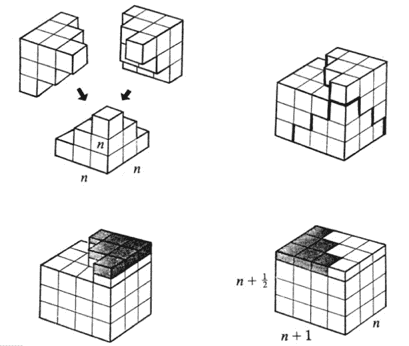
The sum of first n squares
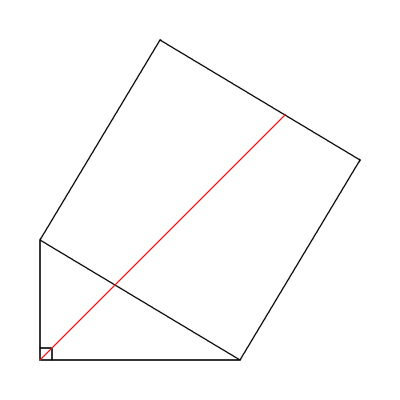
Half and half
A line that bisects the right angle in a right triangle also bisects a square erected on the hypotenuse.