Many people believe math is boring, but in reality — it’s anything but. Here, we’ll be looking at some of the most intriguing mathematical facts, the kind of facts which just make you tilt your head and wonder how they can be even possible.
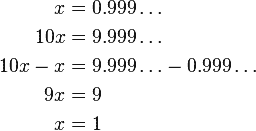
0.999… is equal to 1
This is a hard one to wrap your head around. 0.999… with infinite decimals, often written as 0.(9) is actually equal to 1. How does that work? Well, there’s a couple of ways you can look at it.
Firstly, one divided by three is 0.333…, with infinite decimals. Then, 0.(3) multiplied by 3 is 0.(9)… but it’s also 1 because a number multiplied and divided by the same number remains unchanged. To put it mathematically:
1:3 = 0.333, or 0.(3)
0.(3) x 3 = 0.(9),
but 1:3*3 = 1, so 1 = 0.(9).
You can also think about it this way:
If that’s not convincing enough, then think about it another way. If 0.(9) is smaller than 1, then what would you have to add to it to get to 1? No matter what number you add, it’s still not small enough because such a number doesn’t exist – 0.999… = 1.
111111111 * 111111111 = 12345678987654321

Now this one almost seems made up. By multiplying numbers made of “ones” you end up with a number made of all the figures from 1 to 9 and back to 1. More properly, it would be written like this:
111,111,111 * 111,111,111 = 12,345,678,987,654,321
It still doesn’t seem to make much sense, but it does if you take it step by step. So:
1*1 = 1. Of course.
11 * 11 = 121. Hmm…
111 * 111 = 12,321. A pattern is starting to emerge.
1,111 * 1,111 = 1,234,321. Ok, you probably get the idea by now. Just to finish the whole thing:
11,111 * 11,111 = 123,454,321,
111,111 * 111,111 = 12,345,654,321,
1,111,111 * 1,111,111 = 1,234,567,654,321,
11,111,111 * 11,111,111 = 123,456,787,654,321, and of course:
111,111,111 * 111,111,111 = 12,345,678,987,654,321. There you have it!
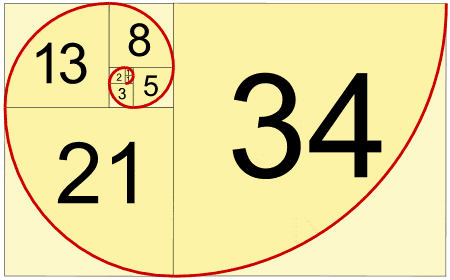
The Fibonacci sequence is encoded in the number 1/89
The Fibonacci sequence is one of the most beautiful things in mathematics. It’s a series in which every number is composed of the sum of the previous numbers, starting with 1. It goes like this:
1 (starting number)
1 (starting number)
2 (1+1)
3 (2+1)
5 (3+2)
8 (5+3)
13 (8+5)
… and so on. So what does 89 have to do with it? Nothing at a first glance. 1/89 is an infinite number which can be written as:
1/89 = 0.01 + 0.001 + 0.0002 + 0.00003 + 0.000005 + 0.0000008 + 0.00000013 + 0.000000021 + 0.0000000034… and so on, enclosing in it the entire Fibonacci sequence, to infinity and beyond.
At a first glance, that seems like an uncanny coincidence, but it’s not. It comes from the fact that 1/(1-x-x2) generates a Fibonacci sequence. Replace x with 1/10, and you end up with 89. Voila!
The Fibonacci sequence pops up in nature. A lot!
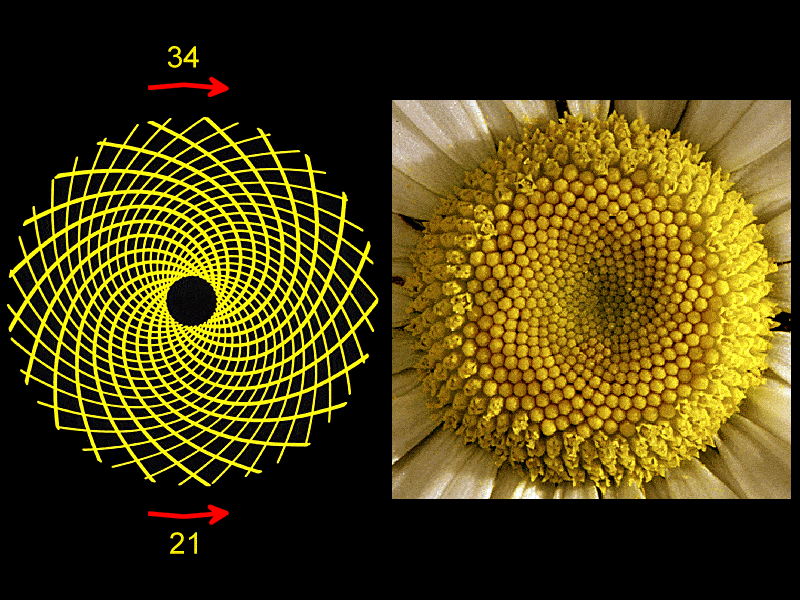
While we’re at it, we really have to discuss the Fibonacci sequence more. First formally described by a mathematician called Leonardo Pisano who was born in 1175, its name comes from a misreading of Pisano’s mention – son of Bonaccio – from a manuscript.
Pisano first described the sequence while describing a problem about rabbit multiplying, which is fitting because the sequence pops up in nature a lot. For example, the number of petals on a daisy is always a Fibonacci number: 21, 34 or 55. Fibonacci sequences also emerge on sunflowers, pine cones, shells, hurricanes and even spiral galaxies!
Euler’s identity:
Often called “the most beautiful equation” and likened to a Shakespearean sonnet or a da Vinci picture, Euler’s identity is beautiful because it manages to encompass the five neutral constants in mathematics:
0 – the neutral element for addition and subtraction,
1- the neutral element for multiplication and division,
e – Euler’s number, the base of natural logarithms,
i – the imaginary unit, which satisfies i2 = −1, and
π is pi, the ratio of the circumference of a circle to its diameter.
It’s impossible to comb all the hairs on a tennis ball in the same direction

The theorem was first stated by Henri Poincaré in the late 19th century, and there is a much more proper way to mathematically formulate it: “there is no nonvanishing continuous tangent vector field on even-dimensional n-spheres.” Colloquially though, it is expressed in a much simpler way: “you can’t comb a hairy ball flat without creating a cowlick”.
This theorem, which was proven in 1912 by Brouwer has an interesting consequence: in an ideal spherical planet, there is at least one point in which the wind is blowing. The planet doesn’t even need to be perfectly spherical, just needs to be continuous — as in not have a hole in the middle like a doughnut.
Six weeks lasts exactly 10! seconds
In case you’re not a math guy, that doesn’t mean ten excited seconds, that’s ten factorial, which is 1 * 2 * 3 * 4 * 5 * 6 * 7 * 8 * 9 * 10. There’s a really nice way to visualize this. There are:
3*4*5 seconds in a minute
6*10 minutes in an hour
8*√9 hours in a day
7 days in a week
2*√9 weeks in six weeks.
(Explanation: √9 is 3, and √9 * √9 = 9, so you end up with 1 * 2 * 3 * 4 * 5 * 6 * 7 * 8 * 9 * 10, which is 10!).
The decimal fractions of seven are the same six recurring digits, in the same order, but starting from a different one
1/7 = 0.142857142857…
2/7 = 0.285714285714…
3/7 = 0.428571428571…
4/7 = 0.571428571428…
5/7 = 0.714285714285…
6/7 = 0.857142857142…
If you really shuffle the cards in a deck, there’s a good chance you end up with a configuration no one ever created
We think card games are pretty limited because there are only 52 cards, but it’s ridiculous how many combinations you have in these 52 cards. There are, of course, 52! possible combinations (remember the factorial thing above?), which is a humongous number: 80658175170943878571660636856403766975289505440883277824000000000000.
That number is beyond astronomically large, but that’s exactly how many ways you can arrange 52 cards. So when you’re shuffling a deck, shuffle it properly – you may create a completely new arrangement, one that no one has ever created before.
BONUS: A pizza that has radius “z” and height “a” has volume Pi × z × z × a.

A pizza is basically a very short cylinder, and that’s how you calculate its volume.
This article was inspired by these two Reddit posts.
Was this helpful?