A team at Lawrence Livermore, helped by researchers from all around the world, announced the discovery of five new isotopes, adding to the already extensive list of 3,000 isotopes of 114 confirmed chemical elements. The exotic atomic variations discovered are one isotope each of heavy elements berkelium, neptunium and uranium and two isotopes of the element americium.
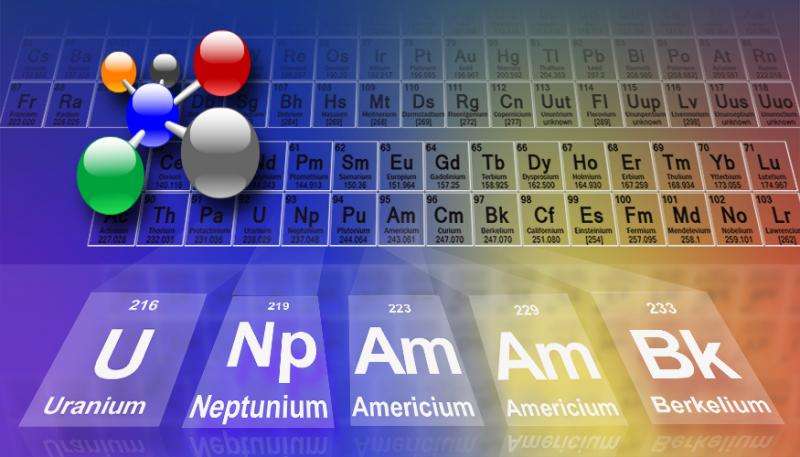
Atoms in a chemical element that have different numbers of neutrons than protons and electrons are called isotopes. Remember ions? Those are variations of atoms with missing or extra electrons. Isotopes are similar, only varying in neutrons – it’s still the same element. Take carbon, for instance. The most stable carbon in the Universe is C-12, which has 6 neutrons. Carbon-14 actually has 8 neutrons (2 extra), and as such it’s considered an isotope.
Now, the thing about isotopes is that they don’t last very long. C-14, for example, will eventually lose its extra neutrons and become C-12 – a process called radioactive decay. Some take longer to decay, while other isotopes transform in a flash! The experiments at the Lawrence Livermore lab are a prime example. Here, researchers shot at a 300-nanometer-thick foil of curium with accelerated calcium nuclei. When the two collided, they formed a compound system for a very short while. Using special filters composed of electrical and magnetic fields you can see what happens at the collision site down to the fraction of a second.
This is how the researchers found the isotopes of berkelium, neptunium, uranium and americium were created as the end products of such collisions. These formed a sextillionth of a second following the collision, and decayed only few milliseconds or seconds later, depending on the isotope. The findings were reported in Physics Letters B.
“These results really push what we know about nuclear structure to the extreme, neutron-deficient end of the chart of the nuclides,” Livermore researcher Dawn Shaughnessy said. “When you realize that naturally occurring uranium has 146 neutrons and this new isotope only has 124 neutrons, it shows how much more we still have yet to learn about nuclear structure and the forces that hold the nucleus together.”
It’s believed 4,000 additional, undiscovered isotopes should exist, and the Livermore researchers hope to add more new isotopes to the chart using the same technique.