The link between art and mathematics spans a very long time. Mathematics has influenced art and art has influenced mathematics for as long as they have existed. In the intricate dance between math and art, the lines often get blurry, and it’s hard to define where one ends and the other begins. But then again, science truly wouldn’t exist without mathematics. Which begs the question, what is mathematics — science, art, or maybe a bit of both?

Art and numbers
The ancient Greek sculptor Polykleitos is regarded as one of the most important sculptors of classical Antiquity. Polykleitos is known not just for his art, but also for his Canon, a book in which he documented the “perfect” body proportions of the male nude: 1/√2 (one over the square root of two).
The Canon itself is lost, but we know from other writings and sculptures that were noted to follow it that it was based on the principles and concepts of Greek Geometry. It’s one of the earliest recorded uses of mathematics in art, but not nearly the only one.
For instance, the “golden ratio” postulated by Euclid (which is approximately equal to 1.618) inspired many artists, from Leonardo da Vinci to Salvador Dali to the Swiss architect Le Corbusier, famous for his contributions to modern architecture. In fact, the list of artists influenced by mathematics goes on for long.
Music is also strongly influenced by mathematics. The ancient Chinese, Egyptians, and Mesopotamians all studied the mathematical principles of sound, while the ancient Greeks went as far as to describe musical scales in terms of numerical ratios, noting that “all nature consists of harmony arising out of numbers”.
From the time of Plato, harmony was considered a branch of math or physics, and as our understanding of sound improved, this approach only became more prevalent. Sounds are defined in terms of frequency, and the frequencies we tend to like can be described mathematically.
| Common term | Example name | Hz | Multiple of fundamental | Ratio of within octave |
|---|---|---|---|---|
| Fundamental | A2 | 110 |  |  |
| Octave | A3 | 220 |  |  |
 | 0 | |||
| Perfect Fifth | E4 | 330 |  |  |
| Octave | A4 | 440 |  |  |
 | 0 | |||
| Major Third | C♯5 | 550 |  |  |
| Perfect Fifth | E5 | 660 |  |  |
| Harmonic seventh | G5 | 770 |  |  |
| Octave | A5 | 880 |  |  |
 | 0 |
Far from being diametrically opposite, math and art often go hand in hand and have influenced each other over the centuries, with math sometimes serving as a “seed” for art or as a tool to define practices and patterns.
More recently, math and art have blended in a new way, with Artificial Intelligence algorithms, based on math, being used to produce art (it is perhaps debatable whether or not this is true art, but the fact that we’re not even sure suggests there’s at least some artistic value to it)

No science without math
Meanwhile, it’s safe to say that without mathematics, we simply wouldn’t have science — or we’d be stuck at the same level we were at thousands of years ago.
Ancient Greeks developed key principles of geometry, which enabled them to do remarkable things like measure the size of the Earth. When Newton developed calculus, we suddenly had a new way to explain and calculate motion, electricity, and even acoustics.
As math became more refined, so too did our understanding of the world around us. New scientific developments pushed our mathematical understanding, and new mathematical understanding paved the way for new scientific developments. Einstein famously predicted the existence of black holes before they could be observed — he even predicted gravitational waves, not confirmed until 2016, a century before we actually observed them.
Nowadays, mathematics is essential in pretty much all sciences. It’s used to study and describe everything from biology to physics, and its evolution is tightly intertwined with science — probably moreso than with art.
But is mathematics itself a science or an art? Or perhaps, both or neither?
Beauty and elegance
The mathematician Benjamin Peirce, who taught at Harvard University for some 50 years called mathematics “the science that draws necessary conclusions.” In one sense, he’s definitely right: mathematics is used to describe the structure and space of the natural world and how things change. As Abel Laureate Dennis Sullivan put it, a better name for mathematics could be “The Logic of Space and Number”.
Meanwhile, mathematician Jerry P. King, who spent forty-five years teaching mathematics at Lehigh University, describes mathematics as an art, stating that “the keys to mathematics are beauty and elegance and not dullness and technicality”. Keep in mind, we’re talking about mathematics as a whole — a calculation of how much money you’ll have at the end of the month is not exactly elegant or beautiful, but some mathematical proofs, like for instance how there are infinitely many prime numbers, or why Pi is an irrational number, can easily be considered beautiful and elegant.
Paul Erdős, one of the most prolific mathematicians of the 20th century, also famously said that numbers are beautiful.
“Why are numbers beautiful? It’s like asking why is Beethoven’s Ninth Symphony beautiful. If you don’t see why, someone can’t tell you. I know numbers are beautiful. If they aren’t beautiful, nothing is”.
Bertrand Russell, whose work was immensely influential in both mathematics and philosophy, echoed these feelings:
“Mathematics, rightly viewed, possesses not only truth, but supreme beauty—a beauty cold and austere, like that of sculpture, without appeal to any part of our weaker nature, without the gorgeous trappings of painting or music, yet sublimely pure, and capable of a stern perfection such as only the greatest art can show.”
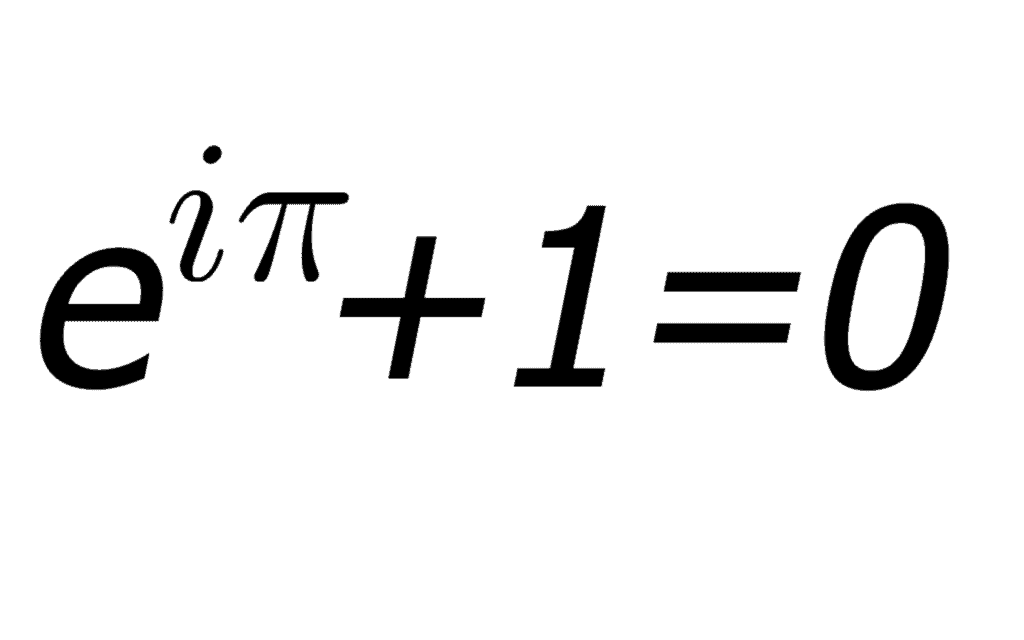
But that still doesn’t really answer the question. Beauty and elegance aren’t necessarily linked to art alone — no doubt, many physicists would describe Maxwell’s equations or much of Einstein’s work as beautiful or elegant. An engineering approach can also be elegant, as can a psychological study.
To answer the question of whether mathematics is science or art, we have to look at what mathematics is. It would be useful to know, for instance, if math was discovered or invented. Unfortunately, this too is a tricky problem to solve.
Some view mathematics as something that’s deeply embedded into the universe which can only be discovered — like atoms or black holes. Others see mathematics as a tool that we construct to help us make better sense of the world around us. Einstein himself took an ambiguous position, noting that “as far as the laws of mathematics refer to reality, they are not certain; and as far as they are certain, they do not refer to reality.”
But perhaps there’s a different way of going about things. In a lecture delivered at the Lindau Nobel Laureate Meetings in 2022, Fields Medal laureate Efim Zelmanov also addressed whether math is art or science, and he started from a different perspective.
“There is another side to mathematics: proof. Or I should say, Her Majesty, proof,” Zelmanov said.
Whether mathematics exists or it needs to be invented, one thing seems clearer: even if it exists, the proofs which we use to show that it is correct are invented. Proofs are integral to all of mathematics, so if we could at least figure out whether proofs are art or science, then we could get closer to solving our big question. But what is a mathematical proof?
There are many formal definitions, Zelmanov explains, but even mathematicians don’t always agree on what is truly a proof. Instead, Zelmanov proposes a different definition:
“In reality, proof is what is conceded to be a proof by all mathematicians. It’s a bit informal, but since I teach students, I know that it is virtually impossible to define what is a proof. Students need to read many proofs and then they will develop this ability to see what is a proof and what is not.”
In the same line of thought, Zelmanov says students of mathematics are taught to recognize beauty, much like students of art are taught to recognize beauty in paintings. Not all proofs are beautiful, which Zelmanov argues makes mathematics even more art-like.
“The purpose of mathematics is understanding. A proof can be beautiful or ugly. This makes mathematics almost an art. If you listen to a conversation between mathematicians, you may think you’re […] hearing 2 artists: this is more beautiful or that is more beautiful.”
“How do mathematicians know what is beautiful and what is not? In the same way as musicians know. In musical schools, they are taught that the music of Mozart, Bach, etc, is beautiful. Students in art schools, they copy paintings of great masters just to develop taste. In the same way, mathematicians learn the work of great predecessors and they develop taste (though some do not). I’m not sure that all modern music would be considered beautiful in the time of Mozart. Maybe it is the same with mathematics.”
Yet even Zelmanov concedes that while art is made for the people, mathematics is enjoyable to far fewer people.
“Mathematics is a very elitist art. How many billions of people can enjoy music and theMona Lisa? How many mathematicians can enjoy a very deep paper in number theory? Maybe 10.”
Zelmanov also adds that mathematicians like simple statements and deep, complex proofs. They like unexpected ideas that come from different ways of thinking, and they like generality. Scientists also do. To an extent, artists also do. So perhaps this says more about the nature of mathematicians than that of mathematics itself.
But if we don’t trust mathematicians to say whether their work is art or science, then who should we trust?
Who decides if mathematics is a science or an art?
Practically, what mathematics is makes little difference. Sure, it matters for things like organizing universities (deciding if the math department should be connected with science departments, for instance), or for deciding whether science grants should also cover mathematics or vice versa.
Also in practice, you’re much more likely to come across someone who does mathematical physics or computational biology than someone who does mathematical art; and yet, you’ll probably come across many mathematicians who’ll say their field is beautiful and artistic.
At the end of the day, it’s hard to put mathematics in a corner, it just shares too many similarities to both art and science. In fact, you could perhaps argue that science and art are mathematics, and not the other way around — science is an application of math to the physical laws in our universe, while art is an application of mathematics to the appeal of the human senses.
Ultimately, there’s no clear answer to whether math is an art or science. It’s a bit of both, but it’s neither quite fully. Mathematics is its own special beast, and there’s something fundamentally fascinating about it — although it takes a bit of familiarity to be able to truly appreciate it.






