The bane of high school (and sometimes university) students, calculus is actually a blessing for mankind — a complex and rather hard to understand one, but still a blessing.
Calculus is a form of advanced mathematics that deals with how things change. It is basically a system of studying how one value changes in relation to another; you may also hear it referred to as “the study of infinitesimals”.
For example, if you know how much money you are receiving and spending every day, calculus can help you understand how much money you’ll have after a number of days. Or, as is the case in many physics problems, you can calculate how long it would take for a car to stop if you know its speed and deceleration. Calculus may be a nuisance, but it’s a very important nuisance.
Oh, and yes — contrary to popular belief, calculus is useful in real life, either directly, or by training your mind to look at things in a scientific manner.
Was calculus discovered or invented?
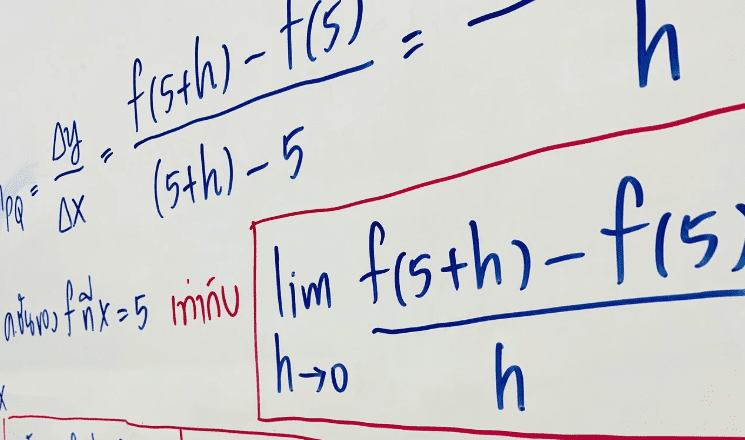
An interesting question that sometimes comes up regarding calculus is whether it was discovered or invented. The question is rather philosophical in nature so it’s hard to answer it one way or another.
Generally speaking, mathematicians speak of discovering a proof or a method, and this also seems to be the case with calculus. Calculus was discovered (or invented) in the late 17th century by Sir Isaac Newton in England and Gottfried Leibniz. The two worked separately and had a bit of rivalry between them, even ending up arguing over who deserves credit for calculus.
Newton, who received the support of British scientists, needed calculus for studying the planets’ movement across the sky, which was important both scientifically (as the field of astronomy was taking off at the time) and practically because it was important for the navigation of ships. Leibniz, who was supported by scientists from the rest of Europe, was more interested in calculating the area under a curve, a challenging problem for mathematicians at the time.
Honestly, it matters little to us who discovered it. Both men were titans of science and mathematics, and both made valuable contributions that are useful to this day.
Truth be told, Newton and Leibniz weren’t the first to dabble with calculus, though they were the first to develop it as a rigorous system. Many ideas in calculus appeared in Ancient Greece, and even before that. Some mentions of ways to calculate volume and area, one of the first goals of integral calculus, appear in the Egyptian Moscow papyrus from over 3,800 years ago. The Ancient Greece mathematician Euxodus discussed the method of exhaustion in the 4th century BC, and Archimedes later built on these methods, developing calculations which resemble calculus. Independently, Chinese mathematician Liu Hui discovered the method of exhaustion (which calculates the area of a shape by inscribing inside it a sequence of polygons whose areas converge to the area of the original shape) seven centuries later, around 300 AD. Many mathematicians from other parts of the world made contributions to calculus, including a foundational treatise by Italian mathematician Bonaventura Cavalieri — but it wasn’t until Leibniz and Newton that we truly had calculus.
The essence of calculus
There are two different types of calculus (differential calculus and integral calculus). The two are inverse operations (somewhat like addition and subtraction, but not quite), and we’ll get to them in a bit. But before that, let’s look at what really makes calculus tick: and that’s infinitesimals.
Let’s say you want to calculate the area under a curve, like Leibniz did. If the curve happens to be a half-circle or some other well-known feature, we’re in luck — we’ve got the formula for that. But what if it’s just a random curve? Well let’s start by being gross about it: let’s approximate the area underneath the curve by a rectangle. Well, as you’d imagine, it’s not very accurate. What if instead of one, we used two or three rectangles of different heights? Well, it’s still not really good, but it’s somewhat closer to the truth.
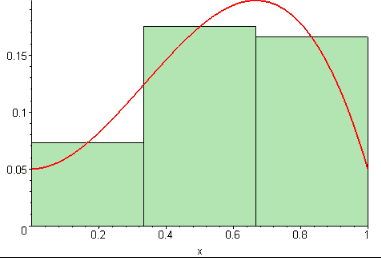
Now what if we add a few more rectangles? We’ll still be off, but the more rectangles we add, the closer we’ll get to approximating the shape under the curve. As we add more and more rectangles, we’ll get closer and closer to the truth. Ultimately, if we add an infinite number of infinitely small rectangles, we’ll get “infinitely close” — which is to say, our approximation is no longer an approximation, it’s the actual curve.
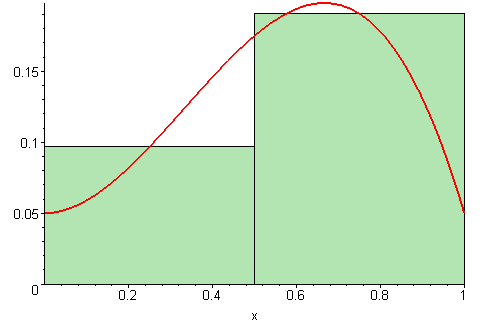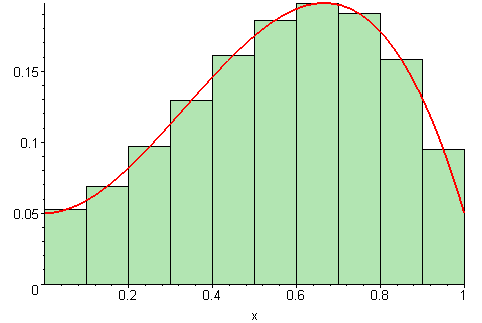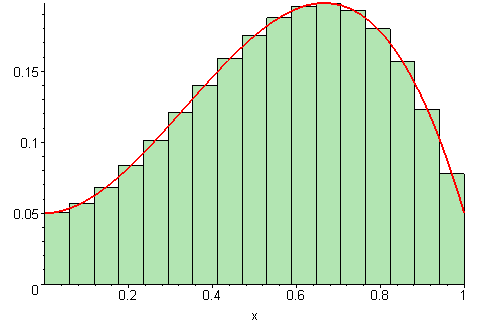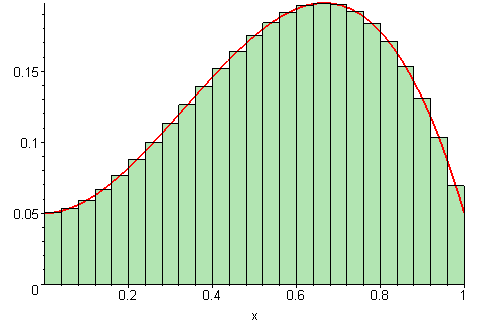
So we have a perfectly algebraic way to calculate complex geometric problems. But this also applies to physical values — the curve could, for instance, be the speed of a car, or the rate at which you’re spending money, and calculus can be of great use here.
Calculus offers a completely new framework of dealing with physical quantities, especially in regards to how they change over time. We can study the path of objects like Newton wanted to, or look at velocity or acceleration. We can even look at more complex things, like the laws of electromagnetism or even Einstein’s theory of general relativity — all of them use calculus.
This way of working with infinitesimals is one of the fundamental building blocks of calculus. Another such building block is limits.
A limit is a value of a function (or sequence) that “approaches” some value without actually reaching. If you want to compare or compute things that are infinitely small, then you need limits. In the above example of the curve, you will have an infinite number of rectangles, but they will be infinitely small. Limits let you work with infinities and zeroes without having the math break down. Let’s take a simple example.
Say you have a function, f(x), that is defined as follows:
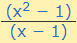
That’s all fine and good, you can calculate your function for almost all values of x with no problem. But what happens when x = 1? Well, your function becomes (1-1)/(1-1), which is 0/0, and as we know, 0/0 is undefined. But let’s say you’re really stubborn and want to get really really close to 1.
Let’s try the same approach as with the curve and do a gross approximation. Let’s say x = 0.5. If we make the calculation, the f(x) is 1.5. If we make x = 0,75 it’s 1,75. Let’s look at a few more values:
| x | f(x) |
| 0.5 | 1.5 |
| 0.75 | 1.75 |
| 0.9 | 1.9 |
| 0.99 | 1.99 |
| 0.999 | 1.999 |
| 0.9999 | 1.9999 |
| 1.0001 | 2.0001 |
Intuitively, you can already see that the function when x = 1 tends to converge around f(x) = 2. We want to say that the answer is 2, but we can’t say it’s exactly 2, so we use limits to say that when x is almost but not quite 1, the answer is 2.
Technically, we can use a limit to calculate when x gets infinitely close to 1 through a limit:
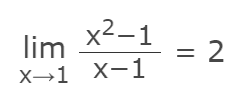
We can also look at this by plotting the function, with the x values on the horizontal, and the f(x) values (or y) on the vertical.
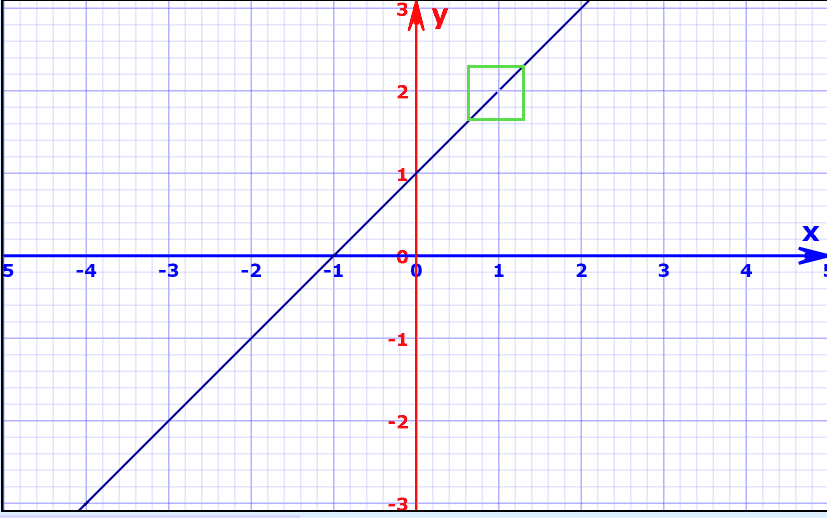
The chart shows a continuous line with one exception, highlighted by the green square: it breaks down when x=1. So in essence, our function is almost 2 when x is almost 1, but it breaks down (is indeterminate) when x is actually 1.
Understanding integrals and derivatives
Now we have the basic tools we need to look at derivatives and integrals — the meat of calculus.
Differential calculus divides things into small different pieces (derivatives) and how they change from one moment to the next, while integral calculus joins (integrates) the pieces together and tells us how much has changed overall.
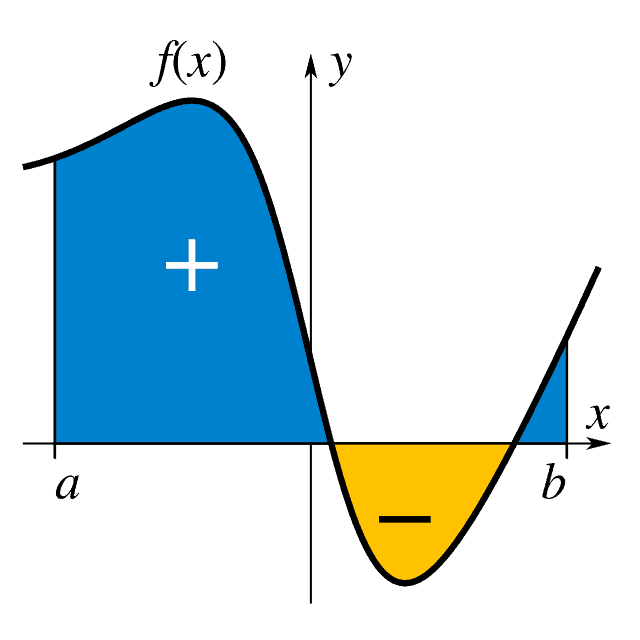
The fundamental theory of calculus binds the two together. If you have a continuous function f, there is a derivative of that function and an anti-derivative, commonly called an indefinite integral (called F), and those two are opposite operations. You can use one to undo the other, just like you can use multiplication to undo division and vice versa. If our function is bound to an interval [a,b], then f is the derivative of F, and F is the integral of f over that particular interval. Essentially:
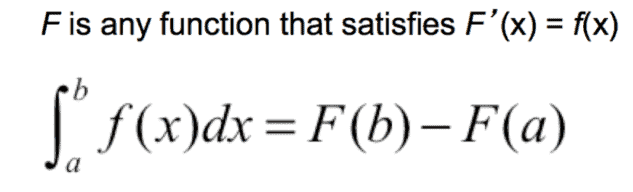
That seems a bit complex, but the good news is that we’ve already done an integral! Remember our example from above, with the curve and the rectangles? Well, in calculus, an integral can be regarded as the space under the graph of an equation — in other words, the area under the curve. In a sense, the integral is a sum; in the case of the area under the curve, it is the sum of all the small rectangles we used to approximate it.
Now let’s see what having an integral over an interval means. In our curve example from before, our interval was “from the start of the curve to the end of the curve”. But it doesn’t need to be from start to finish — we can just pick a start and finish point, and calculate our integral (the area beneath the curve) for that particular part of the curve. Let’s see what that means in graphical form:
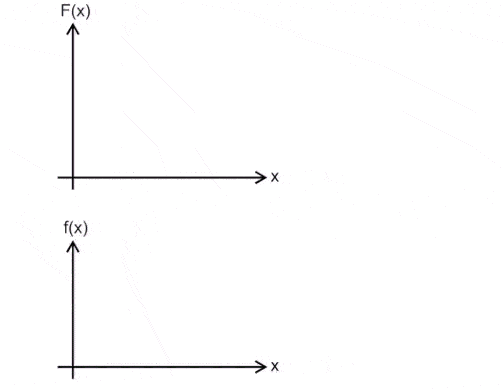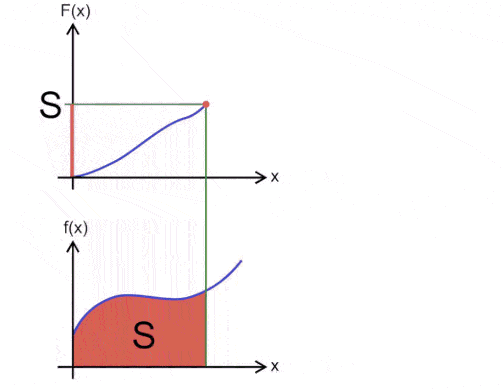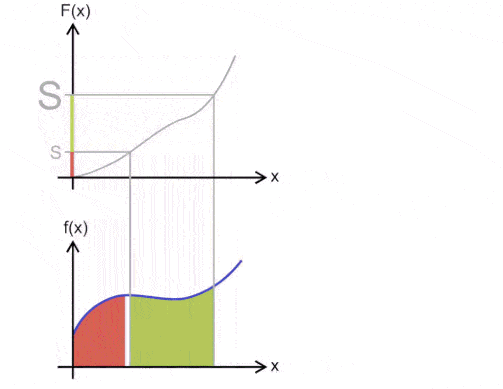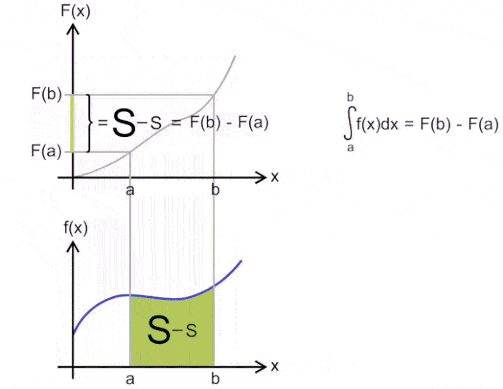
So what does this mean for derivatives?
Well, derivatives measure the rate of change of one value in respect to another — most commonly, of one value in respect to time. The simplest example of derivatives is position, velocity, and acceleration.
Let’s say you’re at some position, and you want to calculate your future position. In order to do that, all you need to know is your velocity — so the velocity is defined as the rate of change of position. Simply put, velocity is the change in position per unit of time, whether it’s miles per hour or meter per second. Conversely, the definite integral of velocity will give us the distance that was covered.
So then, what’s acceleration?
Well, like speed measures the change of position in time, the acceleration measures the change of the speed. So like velocity is the derivative of position, acceleration is the derivative of speed, or the second derivative of position (fun trivia, the third derivative is called jerk or jolt).
Here’s a simple animation of the rate of change versus the curve to help you visualize how the two relate:
How to calculate derivatives and integrals
Now that we’ve hopefully started to understand what derivatives and integrals actually mean, let’s look at how they can be calculated. This is a very complex field in its own right and we’ll only look at the very basics to get you started.
Calculating Derivatives
A derivative is generally defined thusly:
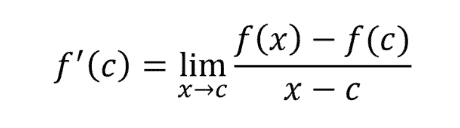
Derivatives are often noted using f(x) and an apostrophe after the f. The notation is f(x) or y´, in some cases. The notations dx/dy or d/dx are also commonly used, especially in physics (or dx/dt, if it is the rate of change in time).
Already, we can draw a few conclusions. For instance, the derivative of any constant value will always be 0. Since the derivative is the rate of change and a constant is not changing, the rate of change will always be 0. The principle is straightforward, but you can actually prove that. If f(x)=c :
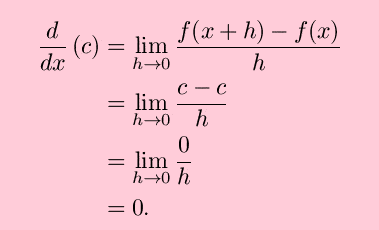
Another takeaway is that when f(x)=x, the derivative will be constant. In other words, x’ = 1; the slope of the line will always be constant. Yet again, we can prove that. If f(x)=x:

From this, you might already have an idea what this means for linear functions of the form ax + b. In this situation, the b doesn’t matter, as it will be 0, and since the derivative of x is 1, then (ax + b)’ = 1. Think of it like the slope of a line: the slope of a constant value is always 0, the slope of 2x is always 2, the slope of 3x is always 3, and so on. Geometry can often help visualize calculus problems.
Derivatives of powers of x are actually pretty straightforward, I’ll give you a hint to see if you can spot the pattern:
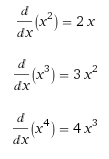
Did you catch it? For every number n, the derivative of x to the power of n will be:
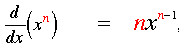
There are ways to compute more complex derivatives (including trigonometric functions), but we won’t get into that here — you’ll find some useful calculus formulas in the following section, but that’s it.
Calculating integrals
Integrals are the inverse of derivatives, so all you need to do to calculate the integral is reverse the derivative. Well, technically speaking, the anti-derivative is the indefinite integral:
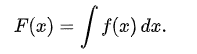
Definite integrals are calculated over a definite interval, as the name implies, so they would look like this:
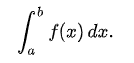
In either case, the first step is calculating the indefinite integral. In the former, that’s the end of the story, whereas in the latter, you have an extra step to do: we calculate the indefinite integral at both a and b, and then subtract them. If we consider F to be the indefinite integral, then:
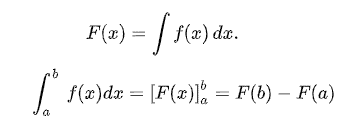
There’s no straightforward way to calculate integrals — unless you memorize integral formulas or have access to them. There are rules of integration, which we’ll address below, but the best way to look at integrals is as the opposite of derivatives. If x’ = 1, then ∫1 = x (a different notation would be F(1)=x). But pay attention to constants! Since this example is an indefinite, and derivatives cancel out constants, there’s no way to know if the derivative had a constant in the first place — so technically speaking, ∫1 = x + c, where c is a constant.
If we were to make that into a definite integral, then it would be integral from a to b. Let’s give another random example and say a=7 and b=10. We calculate F(x) when x=a and F(x) when x=b, and then subtract them. Since our F(x) is actually x, we end up with b – a, or 10 – 7.
If that sounds a bit complex, well, it kind of is. In calculus, as in life, there are no shortcuts and things can be both simple and very, very complicated.
Calculus formulas
Derivative functions
In this notation, the little mark ’ means “Derivative of”, and f and g are functions. The number e is the constant known as Euler’s number.
| Common Functions | Function | Derivative |
|---|---|---|
| Constant | c | 0 |
| Line | x | 1 |
| ax | a | |
| Square | x2 | 2x |
| Square Root | √x | (½)x-½ |
| Exponential | ex | ex |
| ax | ln(a) ax | |
| Logarithms | ln(x) | 1/x |
| loga(x) | 1 / (x ln(a)) | |
| Trigonometry (x is in radians) | sin(x) | cos(x) |
| cos(x) | −sin(x) | |
| tan(x) | sec2(x) | |
| Inverse Trigonometry | sin-1(x) | 1/√(1−x2) |
| cos-1(x) | −1/√(1−x2) | |
| tan-1(x) | 1/(1+x2) | |
| Rules | Function | Derivative |
| Multiplication by constant | cf | cf’ |
| Power Rule | xn | nxn−1 |
| Sum Rule | f + g | f’ + g’ |
| Difference Rule | f – g | f’ − g’ |
| Product Rule | fg | f g’ + f’ g |
| Quotient Rule | f/g | (f’ g − g’ f )/g2 |
| Reciprocal Rule | 1/f | −f’/f2 |
| Chain Rule (as “Composition of Functions”) | f º g | (f’ º g) × g’ |
| Chain Rule (using ’ ) | f(g(x)) | f’(g(x))g’(x) |
| Chain Rule (using ddx ) | dydx = dydududx |
Integral formulas
| Common Functions | Function | Integral |
|---|---|---|
| Constant | ∫a dx | ax + C |
| Variable | ∫x dx | x2/2 + C |
| Square | ∫x2 dx | x3/3 + C |
| Reciprocal | ∫(1/x) dx | ln|x| + C |
| Exponential | ∫ex dx | ex + C |
| ∫ax dx | ax/ln(a) + C | |
| ∫ln(x) dx | x ln(x) − x + C | |
| Trigonometry (x in radians) | ∫cos(x) dx | sin(x) + C |
| ∫sin(x) dx | -cos(x) + C | |
| ∫sec2(x) dx | tan(x) + C | |
| Rules | Function | Integral |
| Multiplication by constant | ∫cf(x) dx | c∫f(x) dx |
| Power Rule (n≠-1) | ∫xn dx | xn+1n+1 + C |
| Sum Rule | ∫(f + g) dx | ∫f dx + ∫g dx |
| Difference Rule | ∫(f – g) dx | ∫f dx – ∫g dx |
So what does calculus do for me?
Well, glad you asked. Let’s get some perspective.
Calculus is a form of advanced mathematics. You won’t need it when you go to the movies or grab a drink with friends (though it could always make for interesting conversations). If you work in any field of science, engineering, finance, or sociology, the odds are that you will come across calculus at some point. But even if you don’t, calculus can be useful in the same way all mathematical education is useful: it helps you understand things.
Calculus is essential in understanding things like change and evolution, in looking at things like interest rates and loans, or even just understanding some of the articles we write here at ZME Science.
Here’s a clear example: the COVID-19 pandemic. We talk about existing patients, new patients, rate of change, survival rate, and to be perfectly frank, even some high-ranking politicians have shown a complete lack of understanding when it comes to these things. If you don’t work in science, you won’t use calculus by writing things on a paper, but you’ll apply the understanding to things in your day to day life, and that can help you grow as a person.






