The humble triangle has been with us from the ancient pyramids to the modern days, being one of the most recognizable, interesting, and useful shapes in geometry. Ancient mathematicians laid the groundwork of geometry by studying triangles, and the shape still terrorizes hapless students to this day.
But there’s more to triangles than meets the eye, and no matter how much you look at triangles, they seemingly still have something to surprise you with. Let’s take a look at some triangle facts.

The modern word triangle draws its roots from the Latin ‘triangulus’ (‘three-cornered’). It is one of the basic shapes in geometry and the simplest one that can define a plane (a 2-D surface).
This three-sided polygon is a marvel of mathematical precision and elegance. As the simplest possible polygon, triangles only sport 3 angles and 3 sides, but they come in many shapes and sizes, as we’ll see shortly. Despite their apparent simplicity, triangles are also very complex — they offer stability and strength, which is why engineers prefer them for many types of constructions, including bridges and buildings.
Triangles also tend to pop up in various fields ranging from biology to mathematics. So let’s dive a bit into their endlessly fascinating world — but before we do that, let’s just clarify that we’ll only be talking about Euclidean geometry. If you don’t know what that is, don’t worry: it’s the non-weird one.
Types of triangles
Based on their sides, triangles can generally be classified as:
- Equilateral: the most aesthetic and “perfect” of triangles. Equilateral triangles have three equal sides and three equal angles of 60°.
- Isosceles: triangles that have two sides of equal length, and two equal inside angles. Their name comes from the Greek words for ‘equal’ and ‘leg’.
- Scalene: with no two sides or inside angles equal, the scalene triangle is the rebel of the lot. Its name comes from the Greek word for ‘unequal’.
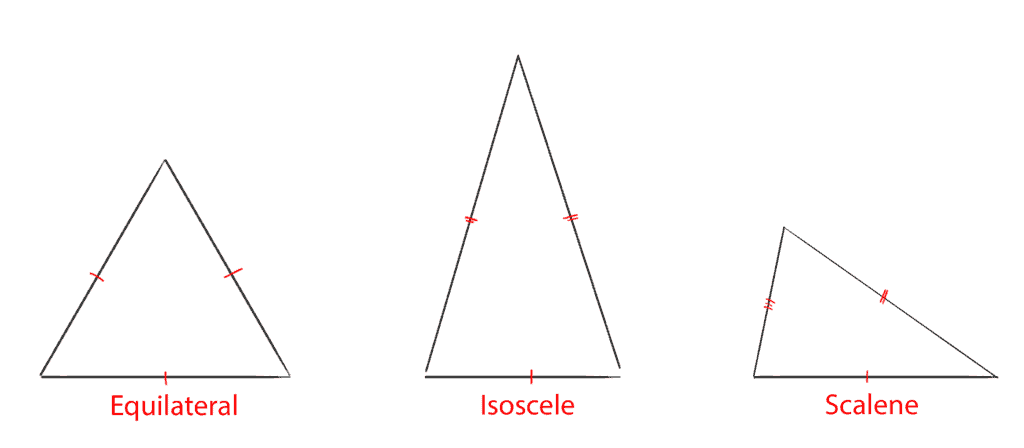
Image credits Alexandru Micu / ZME Science.
Based on their inside angles, they’re can also be classified as:
- Acute: if all internal angles are under 90°.
- Right-angled: if one angle is equal to 90°.
- Obtuse: if one angle is greater than 90°.
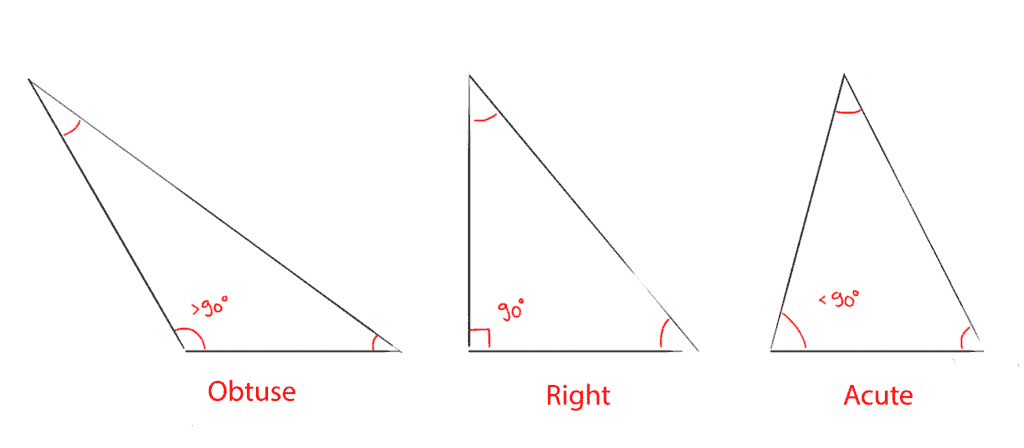
A particular type of triangle is the isosceles right triangle, which has two equal sides and one right angle.
Triangle facts
Triangles have some very handy properties. All simple polygons can be broken down into a series of triangles (even triangles). As a rule, the sum of a triangle’s inside angles is always 180°, and each angle is proportional to the side they oppose, with the longest side always opposite their largest angle (the points of triangles are called vertices or vertexes). The sum of the lengths of any two sides of a triangle is always longer than the third side.
This proportionality lies at the root of the field of trigonometry, which deals with the relationship between face length and the internal angles of triangles. Despite its seemingly niche appeal, trigonometry has a huge range of both practical and theoretical applications, ranging from navigation and the tracking of celestial bodies to the analysis of periodic (cyclic) functions, applied science, engineering, and data compression.
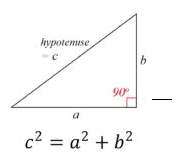
In a right triangle, the side opposite the right angle in a right triangle is called the hypotenuse, and it is the longest side. Perhaps the most famous equation in all of mathematics is related to this: the Pythagorean theory, which states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two. It is possible that the Babylonians and other cultures were also aware of this, but the idea is typically attributed to Pythagoras.
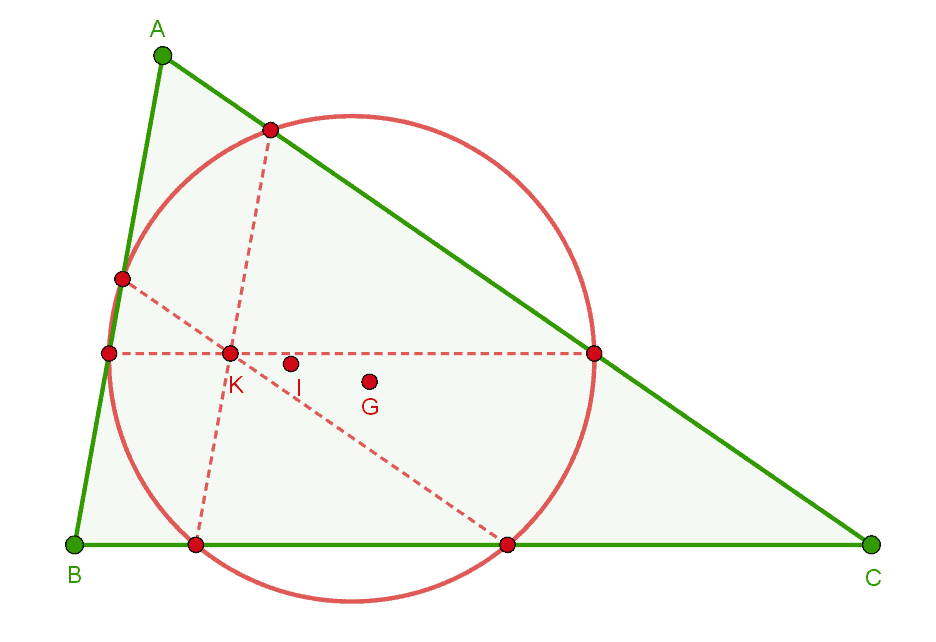
You can draw all sorts of potentially useful lines in triangles. A median, for instance, is a line segment joining a vertex to the midpoint of the opposite side. A bisector is a straight line that bisects an angle (splits it into two equal angles). The point where the three medians of the triangle intersect is called a centroid, and the place where the bisectors meet is called the incenter.
The area of a triangle can be calculated in several ways, depending on what information you have about it. For instance, you can use the classical formula A = 1/2 * base * height, where the base is the length of the bottom side and the height is the perpendicular distance from the base to the opposite vertex. But you can also calculate it using something called “Heron’s formula,” which only uses the length of the sides of the triangle.
Triangles can also be used to derive an endless amount of math problems — some simpler, some difficult; some straightforward, some which require a lot of thought and creativity. But triangles aren’t just significant for mathematics (although indeed, studying triangles is an excellent way of honing your geometrical skills) — they’re important in our day-to-day life, serving as an essential shape, and one that is exceptionally strong.
History of the triangle

We don’t know who first discovered — insofar as a shape can be ‘discovered’ — the triangle. But we do know that mathematicians in Ancient Babylon and Egypt had at least a functional understanding of them.
Geometry means ‘measurement of the earth’ and, being the science of shapes and sizes, was likely first developed out of the need to calculate taxes. The hostile environment of Egypt, coupled with the high fertility of the Nile river, led to the implementation of very centralized agriculture practices. Canals and granaries had to be maintained, seeds and tools distributed to ensure enough food was being produced — all this costs money. Government officials used geometry to calculate cultivated surfaces and make sure that the pharaoh’s taxes were being paid in full. Ancient Egyptians also employed astronomy in support of agriculture by allowing for a more accurate prediction of the Nile’s annual flood. Babylonian knowledge of math and geometry were also quite advanced, mostly derived from their astronomical studies, agriculture, and bookkeeping.
Around 2900 BC, the first of Egypt’s pyramids were constructed. These monuments are a remarkable feat of know-how and engineering. In order for a pyramid to actually be a pyramid, the triangles that make up its faces need to slope at exactly the same angle as the others. Since the monuments were built in successive layers starting from the bottom, engineers had to constantly measure and adjust the works with a high degree of accuracy; not easy to do with the tools of the time. Still, we haven’t found any evidence that Egypt’s geometers academically deduced the properties of triangles. They probably worked through observation and solving practical problems. In essence, they were studying applied mathematics.
But, as it tends to happen in history, the Greeks came around and started thinking about things. Thales of Miletus (624–547 BC) is credited with bringing geometry from Egypt into Greece and laying some early groundwork for the study of triangles. Pythagoras, whose famous theorem is still in use, is hailed as the first ‘pure mathematician’ to study geometry by applying abstract mathematical concepts. Later on, Euclid of Alexandria (325–265 BC) wrote a 13-book treatise titled The Elements.

Image credits Galileo’s World.
Calling it one of the most important books in Western history wouldn’t be out of place; The Elements still defines most geometric study today (the Euclidean geometric system). What set it apart was that Euclid started with a set of basic data — 23 definitions, 5 general axioms — and a set of 5 postulates (theories). An axiom is a statement that is accepted as self-evident and true without needing proof. Euclid then used the data to provide mathematical proof for his first postulate, which in turn was used to prove his second, and so on (but not his fifth, the ‘parallel postulate‘). His work was so groundbreaking that it underpinned all geometrical study until Carl Friedrich Gauss (1777–1855) and others independently developed non-Euclidean geometry.
The difference between classical (Euclidean) and non-Euclidean geometry largely stems from the parallel postulate. Classical geometry starts from the assumption that parallel lines never meet and that they stay at a constant distance from one another; in non-Euclidean geometry, this isn’t the case. Boiled down, classical geometry works in flat planes, while non-Euclidean geometry operates in curved (elliptical or hyperbolic) planes.
In a non-Euclidean system, triangles don’t abide by the same laws. Imagine drawing a triangle on a flattened balloon — that’s classical geometry. But if you inflate it, the triangle deforms onto a spherical plane, which alters its sides and angle values.
During the Middle Ages and the Renaissance, scholars continued to study triangles, making important contributions and using triangles in fields ranging from astronomy to art. As physics and mathematics continued to develop, triangles continued to play a pivotal role in shaping thought and defining theories; and science hasn’t stayed still.
Modern triangle geometry is a field of active research. Triangles and their properties were the subject of investigation since at least the time of Euclid, but somehow, researchers are still finding new points of interest regarding triangles, or are using triangles as tools to study other elements.
No doubt, the humble triangle has been an important point of focus for scholars and students for generations — and will continue to be so for many more generations to come.






