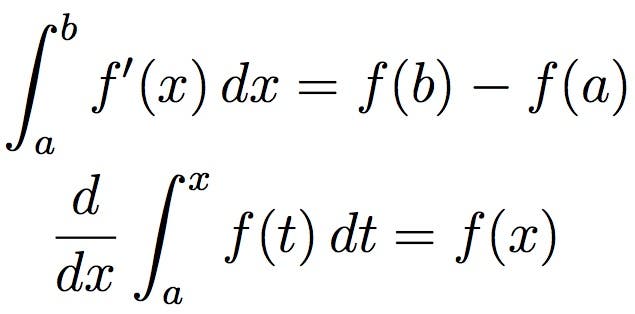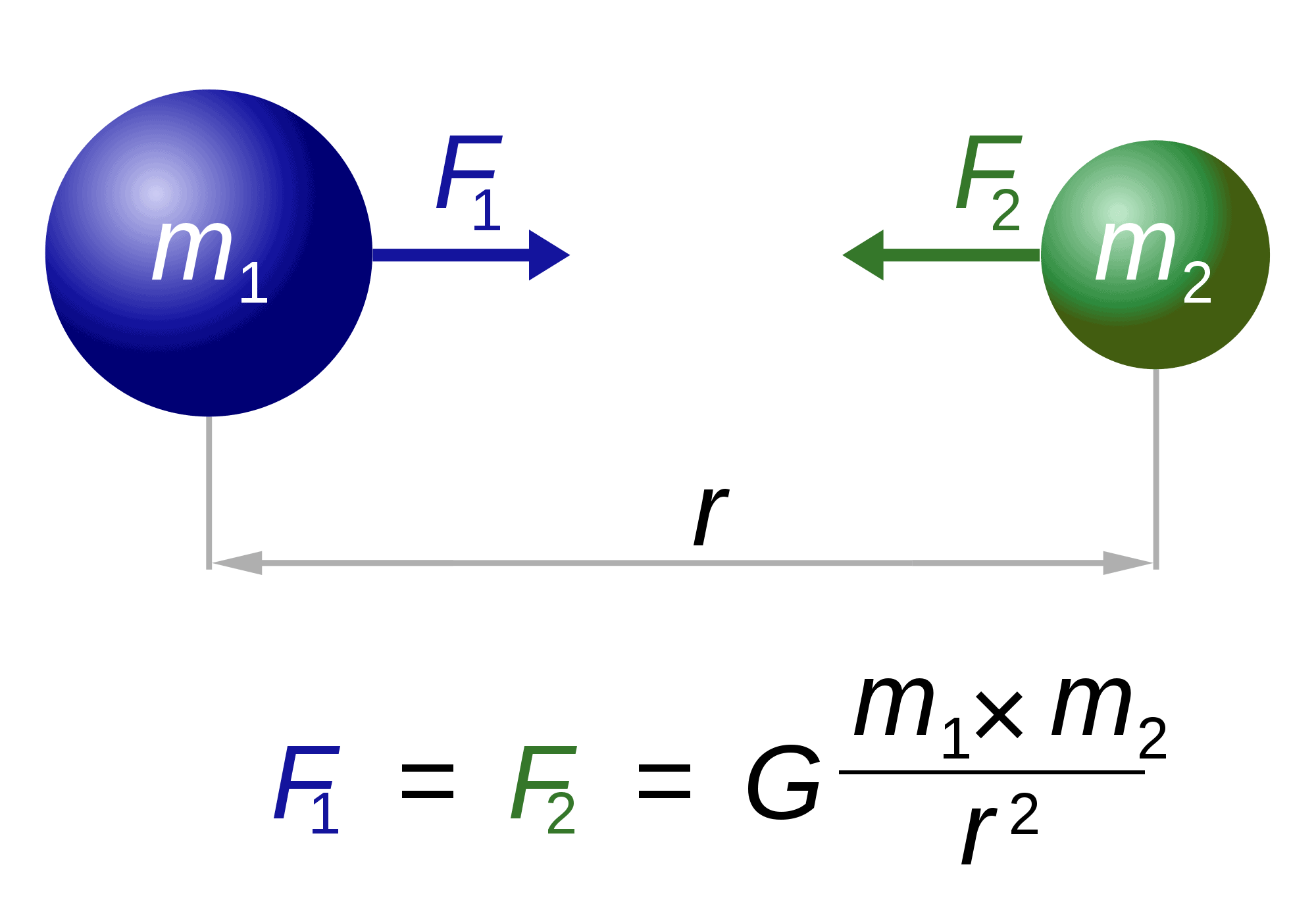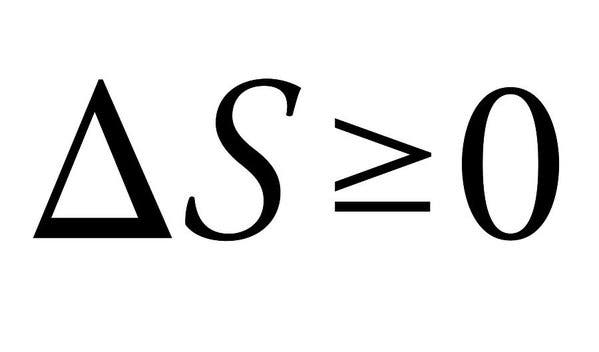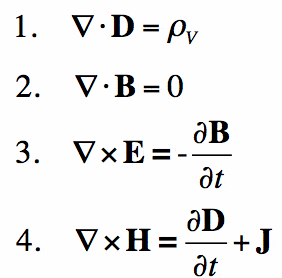Math is more of a marathon than a sprint — it’s a long, slow, and steady grind, with rare and satisfying moments of breakthrough. But once in a when those prized “Eureka” moments do come, they change science forever. These moments often come in the form of equations — mathematical relationships that tie in different elements. Scientists often describe some of these equations as “beautiful” or “elegant” because in addition to being so impactful, they are concise and “clean.”
Here are some of the most famous equations, from the ancient Greeks to modern physics.
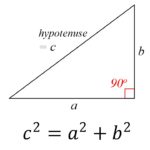
The Pythagorean Theorem (530 BC)
This pretty one of the founding pillars of all geometry: in a right triangle, the square of the hypotenuse (the side opposite to the right angle) is equal to the sum of the squares of the other two. The theory is generally attributed to the Greek mathematician Pythagoras, though there is some evidence that Babylonian mathematicians also understood the formula, and did so before Pythagoras. It’s also very possible that the theorem was known by several cultures, but he was the first to prove it and leave the evidence in writing.
The theorem has been given numerous proofs — possibly the most for any mathematical theorem. They are very diverse, including both geometric proofs and algebraic proofs, with some dating back thousands of years.
To this day, the Pythagorean theorem quite literally defines how we measure distances. It can be generalized to non-right triangles, to objects that are not triangles at all, and even to higher-dimensional spaces. The theorem has a huge number of applications and it plays a role in most if not all fields of mathematics. No doubt, it’s one of the most elegant equations of all time.
Complex numbers (1545)
Complex numbers are the bane of many math students because they’re pretty hard to wrap your head around at first. Complex numbers are numbers that don’t really exist, but that are very useful for a number of calculations. Yes, mathematicians really love inventing things and finding tricks, and complex numbers are a great example of that.
They consist of numbers with a real part (the numbers we all know) and an imaginary part (the i represented here) and have practical applications in many fields, including physics, chemistry, biology, economics, electrical engineering, and statistics. No squared number can produce a negative result, but if you square the complex number i, you get -1. So that’s essentially how i is defined, as the square root of -1. Subsequently, all complex numbers are defined with the help of i.
The Italian mathematician Gerolamo Cardano is the first known to have introduced complex numbers, calling them “fictitious” at the time. However, the mathematical development of “i” as the imaginary number representing the square root of -1 is attributed to Leonhard Euler, one of the most important mathematicians and scientists in human history.
Logarithm equations (1614)
Logarithms are basically the inverse function of exponentiation. Logarithms are also something that is not essentially new, but it helps a lot with calculations. In mathematics, simple tricks can get you a long way.
You need a number (N), a base (a), and the logarithm of N in base a will be x, where N equals a to the power of x. It might seem like only a different way of writing the same thing (and in a sense, it is), but logarithms have a myriad of practical applications, being used in psychology, economy, and measurements of many physical phenomena (such as pH or earthquake magnitude).
Logarithms were publicly propounded by John Napier in 1614, in a book titled Mirifici Logarithmorum Canonis Descriptio (Description of the Wonderful Rule of Logarithms) — a fitting title. A special case of a logarithm is the natural logarithm — e, where e is an irrational and transcendental number approximately equal to 2.71828182845. In fact, e itself has a fascinating history and an impressive number of applications, but that’s a story for another time.
Calculus equations (late 17th century)
Few fields of mathematics have been as impactful as calculus. Developed independently in the 17th century by Isaac Newton and Gottfried Wilhelm Leibniz, calculus is widely used in science, engineering, and economics.
Calculus essentially focuses on dealing with infinitesimally small quantities — numbers that are extremely close to zero, but are not exactly zero. Through calculus, these can be treated as real numbers, even though they are technically infinitely small. For a simpler visualization, integration, depicted above, can be thought of as measuring the area under a curve, defined by a function.
The Law of Gravity (1687)
Speaking of Newton, he is also “responsible” for one of the world’s most famous and spectacular equations: the law of gravity.
The law basically describes how any two bodies of masses m1 and m2 are attracted to each other. The force (F1, F2) is inversely proportional to the square of the distance between them (r). The only remaining factor, G, is a gravitational constant. The nature of this constant remains elusive.
General Relativity (1916)
For almost 200 years, Newton’s law defined our level of understanding of mechanics. Einstein’s work in the 20th century took things to the next level — these two achievements tower on the highest pedestals in the world of physics.
General relativity is essentially a geometric theory of gravitation, generalizing Newton’s theory providing a unified description of gravity as a geometric property of space and time — or spacetime. In particular, Einstein showed not only that there is such a thing as “spacetime” merging the three dimensions with the 4th dimension of time, but he also showed that this spacetime can be curved by gravity, with the curvature being directly related to the energy and momentum of whatever matter and radiation are present.
The Second Law of Thermodynamics (1850)
The Second Law of Thermodynamics is why we can’t have nice things in the Universe. Jokes aside, the four laws of thermodynamics define fundamental physical quantities (temperature, energy, and entropy) that characterize thermodynamic systems. The second one, in particular, stands out here due to its simplicity, but absolutely massive implications.
The law essentially states that the sum of the entropies of the interacting thermodynamic systems must always increase, or at the very most remain constant. When energy changes from one form to another or matter moves around, the entropy (or disorder) in a closed system increases. All differences in temperature, pressure, and density tend to flat out after a while
Maxwell’s Equations (1862)
Simply put, Maxwell’s equations are to electromagnetism what Newton’s law is to mechanics. They provide a mathematical foundation for classical electromagnetism, classical optics, and electric circuits. They are widely used in the very device you are reading this on — basically, all electronic devices.
Maxwell’s laws describe how electric and magnetic fields are generated by charges, currents, and changes in the fields. A significant breakthrough was the demonstration that electric and magnetic fields propagate at the speed of light.
Euler’s Identity (18th century)
Lastly, this is quite possibly the most elegant equation, a thing of supreme beauty, because it involves all the “basic” numbers:
- 0, which is neutral for addition and subtraction;
- 1, which is neutral for multiplication and division;
- e, which is Euler’s number (see above), the base of natural logarithms;
- i is the imaginary unit (see above); and
- π is pi, the ratio of the circumference of a circle to its diameter.
Finding a relation that unifies all these numbers is nothing short of breathtaking, and seems quite unlikely. The demonstration isn’t exactly simple, but you can see it here.
It’s only fitting that Stanford University mathematics professor Keith Devlin described the equation, saying that “like a Shakespearean sonnet that captures the very essence of love, or a painting that brings out the beauty of the human form that is far more than just skin deep, Euler’s equation reaches down into the very depths of existence”
It’s not often that mathematics and physics boil down to simple and elegant equations — but when they do, it’s quite a sight to behold.
Was this helpful?