
Crystals are solid substances where atoms, molecules, or ions are packed in a highly ordered and repeating pattern extending in all three dimensions. This special arrangement not only bestows crystals with their mesmerizing geometric beauty but also underpins a vast array of physical properties that define the material world around us.
Although crystals manifest in an astonishing variety of forms, they each belong to one of seven distinct crystal systems. These systems, ranging from the highly symmetrical cubic system to the less orderly triclinic system, underscore the rich diversity and complexity inherent in the mineral kingdom. Let’s dive in.
Overview of the main types of crystal geometries
The geometry of crystals can get very complicated very fast. Before we explore it in detail, let’s mention the main types of crystals and their main characteristics.
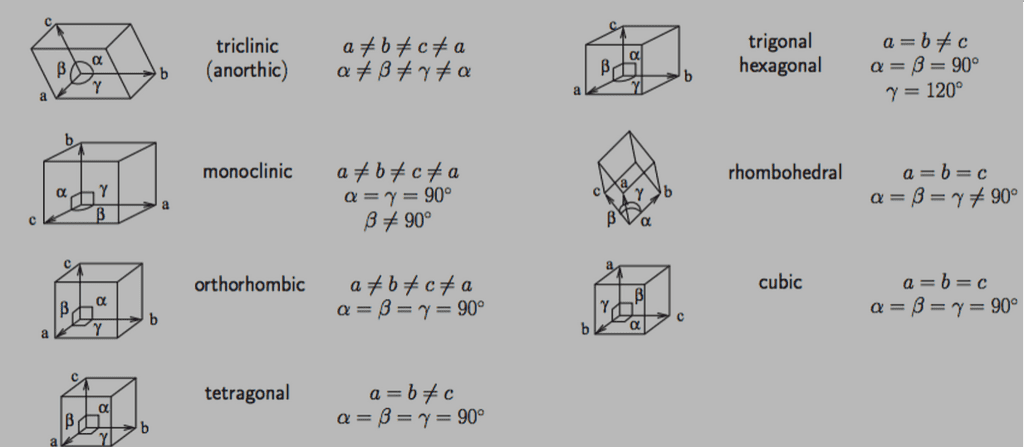
The seven types of crystal systems are:
- cubic (or isometric), where the crystal axes are of equal length and meet at right angles;
- tetragonal, with two equal axes and one longer or shorter axis, all intersecting at right angles;
- orthorhombic, featuring three different axes all intersecting at right angles;
- hexagonal, with four axes where three are of equal length and lie in the same plane at 120-degree angles to each other, and the fourth axis is perpendicular;
- trigonal (or rhombohedral), similar to hexagonal but with a threefold axis of symmetry; monoclinic, with three axes of unequal length, two intersect at right angles, and the third axis meets the others at an angle other than 90 degrees;
- and triclinic, where all three axes are of different lengths and meet at angles that are not 90 degrees.
Basic Crystallography
Crystallography is the science of crystals and their arrangement of atoms, molecules, or ions within a structured grid, known as a lattice. This discipline bridges geology, physics, chemistry, biology, and materials science. Its main aim is to unravel the atomic and molecular structures of crystalline materials.
A crystal’s atoms are arranged in a repeating lattice structure due to the principles of minimum energy and maximum stability that govern atomic interactions. In the solid phase, atoms, ions, or molecules tend to arrange themselves in the most stable, lowest energy configuration possible, which results in a periodic and orderly pattern extending in all three spatial dimensions.
This arrangement minimizes the potential energy of the system by optimizing the distances and angles between neighboring particles, leading to strong, stable chemical bonds and a rigid structure.
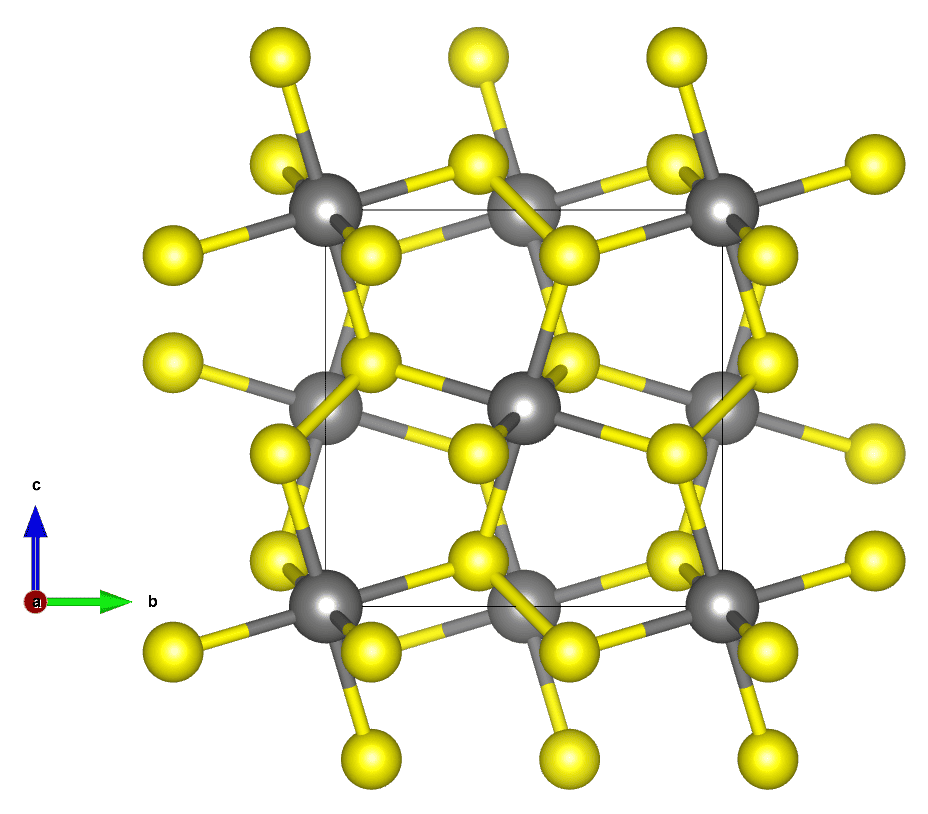
The repeating lattice not only defines the internal structure of the crystal but also influences its macroscopic shape, physical properties, and the way it interacts with light and other forms of energy. This orderly pattern is a fundamental characteristic of crystalline materials, as opposed to amorphous materials, such as glass, where atoms are arranged in a more random and less structured manner.
This knowledge not only provides insights into the geology of crystals but also has practical applications in various fields. These include mineralogy, pharmacology, and nanotechnology, making crystallography a cornerstone of science and technological advancement.
Types of Crystal Systems

Crystals are grouped into seven primary systems, each distinguished by its degree of symmetry and the lengths and angles of its lattice axes. These systems form the backbone of crystallography.
Cubic or Isometric System
The cubic system is characterized by its high degree of symmetry, with three axes of equal length intersecting at right angles. This system is epitomized by minerals such as pyrite (FeS₂), known for its perfect cubic crystals, and diamond (C), renowned for its hardness and brilliance. The cubic system includes geometries such as the cube, octahedron, and dodecahedron, each displaying a unique set of faces that are symmetrical across multiple axes.
- Examples of crystals in the cubic system: Pyrite (FeS₂), Diamond (C), Garnet (general formula: X₃Y₂(SiO₄)₃), and Galena (PbS).
Tetragonal System
In the tetragonal system, crystals have two axes of equal length and a third axis that is either longer or shorter, but all three intersect at right angles. This system allows for a variety of shapes, albeit with less symmetry than the cubic system.
- Examples of minerals in the tetragonal system: Zircon (ZrSiO₄), Rutile (TiO₂), and Scheelite (CaWO₄).
Orthorhombic System
The orthorhombic system features three axes of differing lengths, each intersecting at right angles. Minerals in this system typically produce elongated or tabular crystals. Despite its lower symmetry, the orthorhombic system offers a rich diversity of crystal forms.
- Examples of crystals in the orthorhombic system: Olivine ([(Mg, Fe)₂SiO₄]), Topaz (Al₂SiO₄(F,OH)₂), and Aragonite (CaCO₃).
Hexagonal System
This system is defined by four axes—three of equal length intersecting at 60-degree angles in a plane, and a fourth perpendicular axis of a different length. The hexagonal system is notable for its six-fold symmetry axis.
- Examples of crystals in the hexagonal system: Beryl (Be₃Al₂Si₆O₁₈) and Apatite (Ca₅(PO₄)₃(F,Cl,OH)).
Trigonal System

A subdivision of the hexagonal system, the trigonal system features crystals with a single three-fold axis of rotation. Crystals of this nature typically display rhombohedral or scalenohedral crystal forms. This system bridges the gap between hexagonal symmetry and more complex crystallographic behaviors.
- Examples of crystals in the trigonal system: Quartz (SiO2) Calcite (CaCO₃), Cinnabar (HgS), and Rhodochrosite (MnCO₃).
Monoclinic System2
Monoclinic crystals have axes of unequal lengths, with two intersecting at right angles while the third is inclined. This system has mis that tend to form prismatic or tabular crystals. The monoclinic system is characterized by its lack of high-symmetry orientations.
- Examples of crystals in the monoclinic system: Gypsum (CaSO₄·2H₂O), Orthoclase (KAlSi₃O₈), and Clinopyroxene (general formula: (Ca,Mg,Fe,Al)(Si,Al)₂O₆).
Triclinic System
The triclinic system, with no axes of equal length and none intersecting at right angles, represents the least symmetrical crystals. Minerals in this system tend to produce irregular or distorted forms. This system exemplifies the diversity and complexity of crystal structures.
- Examples of crystals in the triclinic system: Turquoise (CuAl₆(PO₄)₄(OH)₈·4H₂O), Kyanite (Al₂SiO₅), and Albite (NaAlSi₃O₈).
Properties of Crystals
The mesmerizing beauty and the vast array of physical properties of crystals are a direct result of their internal ordered structures. Here are some key properties:
Optical Properties
Crystals interact with light in unique ways, a characteristic that is crucial in applications ranging from jewelry to optical instruments. Birefringence, for example, is a property exhibited by crystals like calcite, where a single light ray entering the crystal is split into two rays, each traveling at different velocities. This phenomenon is used in polarizing microscopes and optical devices. The color of crystals can also be intrinsic, due to the presence of certain elements, or induced, as seen in colored diamonds where structural defects or impurities alter the crystal’s color.
Mechanical Properties
The hardness of a crystal, a measure of its resistance to scratching or indentation, varies widely among minerals. Diamond, the hardest known natural material, owes its unparalleled hardness to the strong covalent bonding between its carbon atoms arranged in a cubic crystal structure. Cleavage and fracture properties describe how a crystal breaks or splits along certain planes. These characteristics are critical in gem cutting, mineralogy, and materials science.






