That’s 10 followed by 250 zeros by the way. That’s not one million or one billion, but roughly on unquadragintillion — a number so big it exceeds the number of particles in the Universe. Gives to show how incredibly complex a deceivingly simple question like “how many ways can you arrange 128 tennis balls” can be. The approximate solution, however, might serve a lot of practical uses from artificial intelligence to predicting when a snow or sand avalanche will happen (by the way, can you imagine in how many ways trillions of sand particles can be arranged?).

Stefano Martiniani, a Benefactor Scholar at St John’s College, University of Cambridge, was the lead researchers of the paper published in Physical Review E. He and colleagues were curious to solve this problem because it’s completely general and helps model other problems in granular physics, which deals with the behaviour of materials like soil, sand or snow. “Granular materials themselves are the second most processed kind of material in the world after water and even the shape of the surface of the Earth is defined by how they behave,” Martiniani said.
The sort of computations Martiniani made will help researchers calculate something called configurational entropy. Basic thermodynamics says entropy is a measure of how disordered a system is. Configurational entropy refers specifically to structural disorder. An ice cube is more ordered than water, hence water has higher entropy than the ice cube.
By measuring the configurational entropy of a system, we can measure structural disorder of all of the particles in a system. Theoretically, its possible to predict how an avalanche will move.
First and foremost, for this work you need to work out how many different ways a system can be structured. The arrangements are so numerous for any system comprised of more than 20 particles, that calculations are hopeless. The Cambridge team found a workaround by approximating the number of arrangements.
“The brute force way of doing this would be to keep changing the system and recording the configurations,” Martiniani said. “Unfortunately, it would take many lifetimes before you could record it all. Also, you couldn’t store the configurations, because there isn’t enough matter in the universe with which to do it.”
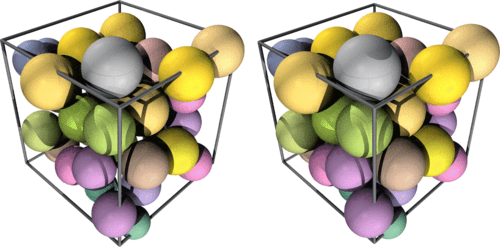
The solution involved taking a small sample of possible configurations of spherical objects (the tennis balls) and working the probability of these occurring — the number of arrangements that would lead to those configurations appearing. By extrapolating, the researchers could approximate how many ways the entire system could therefore be arranged, but also how ordered one state was compared with the next – in other words, its overall configurational entropy.
“The approach that we use computes the configurational entropy by sampling the absolute volume of basins of attraction of the stable packings in the potential energy landscape. We find a surprisingly strong correlation between the pressure of a configuration and the volume of its basin of attraction in the potential energy landscape. This relation is well described by a power law,” the study’s abstract reads.
Although this is a granular physics problem, different versions of the same problem exist in numerous other fields, such as string theory, cosmology, machine learning, and various branches of mathematics.
“Because our indirect approach relies on the observation of a small sample of all possible configurations, the answers it finds are only ever approximate, but the estimate is a very good one,” Martiniani said. “By answering the problem we are opening up uncharted territory. This methodology could be used anywhere that people are trying to work out how many possible solutions to a problem you can find.”






