The amoeba exhibits an unexpected ability to solve the NP-hard problem, taking researchers by surprise.
The Traveling Salesman problem is a fairly straightforward, but pretty complex problem. It can be generally summarized thusly:
“Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city and returns to the origin city?”
The problem is non-deterministic, which means that if you compute an algorithm to solve it, it might come up with different behaviors and solutions, even for the exact same input. In other words, there’s more than one way to approach and solve it (with varying degrees of success).
The researchers, led by Masashi Aono at Keio University, assigned an amoeba to solve the Traveling Salesman Problem (TSP) — and the amoeba performed surprisingly well.
Intelligent amoebas
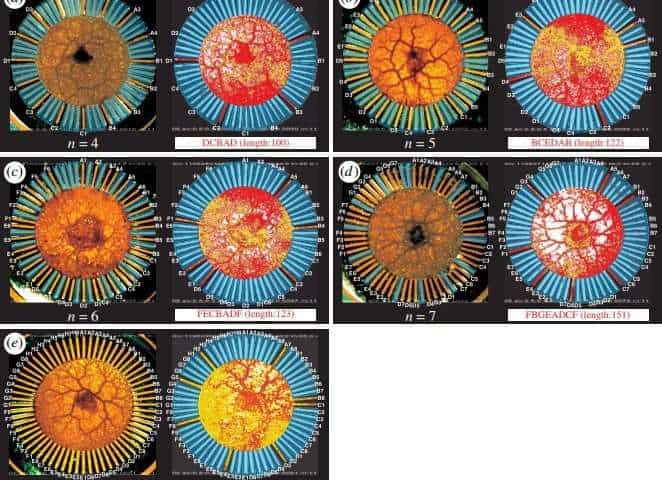
In the experimental setup, researchers placed the amoeba in the center of a stellate chip, which is a round plate with 64 narrow channels projecting outwards. The chip was placed on top of an agar plate — the amoeba was contained on the plate, but it could move through the 64 channels — mimicking the TSP. As the amoeba tried to maximize its nutrient intake, it attempted to reach all the agar plates — but once a channel had been reached, a light was turned on in that particular channel. Since the amoeba doesn’t enjoy the light, it would do its best not to repeat going to the same channel. The chosen amoeba (a plasmodium or “true slime mold”) moved its amorphous body by pushing some of it’s cytoplasm (the liquid inside it) towards it membrane to create pseudopod-like appendages.
Naturally, regardless of the chosen approach, as the number of cities grows, the problem becomes more complex and more difficult to solve. For instance, for 4 cities there are only 3 possible routes. But for 8 cities the number of possible routes increases to 2520. When computers are tasked with this type of problem, the time required to solve it increases linearly. The amoeba also takes more time to solve the problem when the number of cities increases, but the increase happens differently, as the amoeba approaches the problem by redistributing the cytoplasm in its body at a constant rate. It also processes the feedback parallelly, rather than serially, which reduces the necessary time.
Overall, though, the amoeba is still much slower than conventional algorithms and computers, but the fact that the amoeba is able to solve this type of problem is intriguing — perhaps forcing us to reconsider what we know about animal (and in this case, amoeba) intelligence.
“In our stellate chip for solving the n–city TSP, the total area of the body of the amoeba becomes n when the amoeba finally finds an approximate solution,” Aono told Phys.org. “There seems to be a ‘law’ that the amoeba supplies its gelatinous resource to expand in the non-illuminated channels at a constant rate, say, x. This law would be kept even when some resources bounce back from illuminated channels. Then the time required to expand the body area n to represent the solution becomes n/x. This mechanism would be the origin of the linear time, and it was reproduced by our computer simulation model.
“But still, the mechanism by which how the amoeba maintains the quality of the approximate solution, that is, the short route length, remains a mystery. It seems that spatially and temporally correlated movements of the branched parts of the amoeba located at distant channels are the key. Each of these branches is oscillating its volume with some temporal ‘memory’ on illuminated experiences. Groups of the branches perform synchronization and desynchronization for sharing information even though they are spatially distant.”
Researchers expect that the amoeba is able to solve the problem for setups with hundreds of cities — something which would require tens of thousands of channels.
Journal Reference: Liping Zhu, Song-Ju Kim, Masahiko Hara, and Masashi Aono. “Remarkable problem-solving ability of unicellular amoeboid organism and its mechanism.” Royal Society Open Science. royalsocietypublishing.org/doi/10.1098/rsos.180396






