
If you have a straight line but want a circle, you’re going to need some Pi.
I’m talking about the number, not the delicious baked good. It’s usually represented using the lowercase Greek letter for ‘p’, ‘π’, and probably is the best-known mathematical constant today. Here’s why:
The root of the circle
Pi is the ratio of a circle’s diameter to its circumference. No matter the size of a circle, its diameter will always be roughly 3.14 times shorter than its circumference — without fail. This ratio, π, is one of the cornerstones upon which modern geometry was built.
Bear in mind that (uppercase) ∏ is not the same as (lowercase) π in mathematics.
For simplicity’s sake, it’s often boiled down to just two digits, 3.14, or the ratio 22/7. In all its glory, however, pi is impossible to wrap your head around. It is an irrational number, meaning a fraction simply can’t convey its exact value. Irrational numbers include a value or a component that cannot be measured against ‘normal’ numbers. For context, there’s an infinite number of irrational numbers between 1.1 and 1.100(…)001. They’re the numbers between the numbers.
There is no unit of measurement small enough in rational numbers that can be used to fully express the value of irrational ones. They’re like apples and oranges — both fruits, but very different.
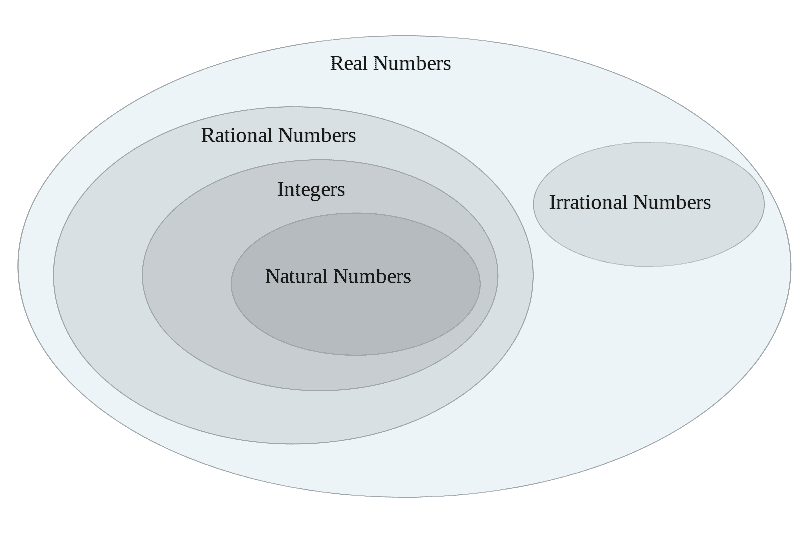
Image credits Damien Karras.
Because it can’t properly be conveyed through a fraction, it follows that pi also has an infinite string of decimals. Currently, we’ve calculated pi down to roughly 22.4 trillion digits. Well, I say ‘we’, but it was actually our computers that did it.
Truth be told, we don’t actually need that many digits. They’re very nice to have if you’re NASA and people live or die by how accurate your calculations are — but for us laymen, 3.14 generally does the trick. It’s good enough because it’s just about at the limit of how accurately we can measure things around us. We simply don’t need that much precision in day-to-day activity.
Go around the house, pick up anything round, and run a length of string along its circumference. Unwind it and measure it with a ruler. Measure the circle’s diameter with the same ruler, use this value to divide the circumference, and you’ll get roughly 3.14 each and every time. In other words, if you cut some string in several pieces, each equal to the diameter in length, you’d need 3.14 of those strips to cover the circumference.
Because this simplification is so widely-used, we celebrate Pi day on March 14 (3/14) every year.
If you do happen to need a more-detailed value for Pi, here it is up to 100 million decimal places.
What’s it for?
Pi is used in all manner of formulas. For example, it can be used to calculate a circle’s circumference (π times diameter), or its area: A=πr2 — how I keep this formula lodged in my neurons is using the “all pies are square” trick. It’s also used in calculating various elements of the sphere, such as its volume (4/3πr3) or surface area (4πr²).
But it also shows up in a lot of engineering and computational problems. Weirdly enough, pi can be used to obtain the finite sum of an infinite series. For example, if you add up the inverse of all natural squares — 1/12+1/22+1/32+….+1/n2 — you get π2/6.
Most branches of science stumble into pi in their calculations at one point or another. Computer scientists use it to gauge how fast or powerful a computer is, and how reliable is its software, by having the device crunch numbers and calculate pi. It’s very useful for determining both circular velocities (how fast something is spinning) as well as voltage across coils and capacitors. Pi can be used to describe the motion of waves on a beach, the way light moves through space, the motion of planets, or to track population dynamics if you’re into statistics.
Another place pi pops up (that you wouldn’t suspect) is in the value of the gravitational constant. This shows how fast an object will accelerate toward the ground as it’s falling. Its most widely-accepted value is 9.8 m/s2. The square root of that value is 3.1305-ish, which is close to the value of pi. That’s actually because the original definition of a meter involved a pendulum that took 1 second to swing either way. Wired has a more comprehensive explanation here.
Pi also underpins modern global positioning systems (GPS) since the Earth is a sphere. So give a little mental thanks to mathematics the next time you’re drunkenly thumbing your phone to hail an Uber.
Who discovered pi?

Pi is not a newcomer to the mathematical stage by any means. We refer to it using the letter ‘π’ from the ancient Greek word ‘περίμετρος’ — perimetros — which means ‘periphery’ or ‘circumference’. It was introduced by William Jones in 1706 and further popularized by Leonhard Euler. The notation was likely adopted in recognition of the efforts of one great ancient mathematician: Archimedes.
Archimedes put a lot of effort into refining the value of pi. He was also the first to use it to calculate the sum of an infinite number of elements over 2,200 years ago, and it’s still in use today.
But he wasn’t the first to realize the importance of pi(e). In his book A History of Pi, professor Petr Beckmann writes that “the Babylonians and the Egyptians (at least) were aware of the existence and significance of the constant π” as far back as 4,000 years ago. They likely only had rough estimations of its exact value (maths was still a new ‘tech’ back then) but they were in the right ballpark.
“The ancient Babylonians calculated the area of a circle by taking 3 times the square of its radius, which gave a value of pi = 3. One Babylonian tablet (ca. 1900–1680 BC) indicates a value of 3.125 for pi, which is a closer approximation,” writes Exploratorium in a look at the history of pi.
They add that ancient Egyptian mathematicians also settled on a quite-ok-for-the-time value of 3.1605, as revealed by the Rhind Papyrus. Chinese and Indian mathematicians also approximated the value of pi down to seven or five digits, respectively, by the 5th century AD.
Further work, most notably that of Archimedes, helped refine this value. He used the Pythagorean Theorem to measure the area of a circle via the areas of inscribed and circumscribed regular polygons. If you slept during math class, that’s the polygon inside the circle and the one that contains the circle, respectively. It was an elegant method, but it did have its limits — since the areas of those two polygons aren’t exactly the same as the surface area of the circle, what Archimedes got was an interval that contained pi. He was aware of this limitation. His calculations revealed that pi must fall between 3 and 1/7 and 3 and 10/71 — which is between 3.14285 and 3.14085. Today we know that the five-digit value of pi is 3.14159, so that result isn’t at all bad for a guy without a proper pen to write it down with.
The first method to calculate the exact value of pi came up during the 14th century, with the development of the Madhava-Leibniz series. By the time the 20th century swang by, pi was known down to about 500 digits.
Was this helpful?