Black holes are cosmic bodies that pack an immense amount of mass into a surprisingly small space. Due to their extremely intense gravity, nothing can escape their grasp — not even light which defines the universe’s speed limit.
April 10th, 2019 marked a milestone in science history when the team at the Event Horizon Telescope revealed the first image of a supermassive black hole. As a result, these areas of space created when stars reach the end of their nuclear fuel burning and collapse creating massive gravitational wells, completed their transition from theory to reality.
This transition has been further solidified since with the revelation of a second, much clearer image of the supermassive black hole (SMBH) at the centre of the galaxy Messier 87 (M87). This second image revealing details such as the orientation of the magnetic fields that surround it and drive its powerful jets that extend for light-years.
The study of black holes could teach us much more than about these spacetime events and the environments that home them, however. Because cosmologists believe that most galaxies have an SMBH sat at their centre, greedily consuming material like a fat spider lurking at the centre of a cosmic web, learning more about these spacetime events can also teach us how galaxies themselves evolve.
The origin of black holes is one that runs in reverse to that of most astronomical objects. We didn’t discover some mysterious object in the distant cosmos and then began to theorise about it whilst making further observations.
Rather, black holes entered the scientific lexicon in a way that is more reminiscent of newly theorised particles in particle physics; emerging first from the solutions to complex mathematics. In the case of black holes, the solutions to the field equations employed by Einstein in his most important and revolutionary theory.
Just as a physical black hole forms from the collapse of a star, the theory of black holes emerged from the metaphorical collapse of the field equations that govern the geometrical theory of gravity; better known as general relativity.
One of the most common misconceptions about black holes arises from their intrinsic uniqueness and the fact that there really isn’t anything else like them in the Universe.
That’s Warped: Black Holes and Their Effect on Spacetime
General relativity introduced the idea that mass has an effect on spacetime, a concept fundamental to the idea that space and time are not passive stages upon which the events of the universe play out. Instead, those events shape that stage. As John Wheeler brilliantly and simply told us; when it comes to general relativity:
“Matter tells space how to curve. Space tells matter how to move.”
John Wheeler
The most common analogy is for this warping of space is that of placing objects on a stretched rubber sheet. The larger the object the deeper the ‘dent’ and the more extreme the curvature it creates. In our analogy, a planet is a marble, a star an apple, and a black hole a cannonball.
Thus, considering this a black hole isn’t really ‘an object’ at all but, is actually better described as a spacetime event. When we say ‘black hole’ what we really mean is an area of space that is so ‘warped’ by a huge amount of mass condensed into a finite point that even light itself doesn’t have the necessary velocity to escape it.
This point at which light can no longer escape marks the first of two singularities that define black holes–points at which solutions of the equations of general relativity go to infinity.
The Event Horizon and the Central Singularity
The event horizon of a black hole is the point at which its escape velocity exceeds the speed of light in vacuum (c). This occurs at a radius called the Schwarzchild radius–named for astrophysicist Karl Schwarzschild, who developed a solution for Einstien’s field equations whilst serving on the Eastern Front in the First World War.
His solution to Einstein’s field equations–which would unsurprisingly become known as the Schwarzschild solution– described the spacetime geometry of an empty region of space. It had two interesting features — two singularities — one a coordinate singularity the other, a gravitational singularity. Both take on significance in the study of black holes.
Dealing with the coordinate singularity, or the Schwarzchild radius first.
The Schwarzchild radius (Rs) also takes on special meaning in cases where the radius of a body shrinks within this Schwarzschild radius (ie. Rs >r). When a body’s radius shrinks within this limit, it becomes a black hole.
All bodies have a Schwarzschild radius, but as you can see from the calculation below for a body like Earth, Rs falls well-within its radius.
That’s part of what makes black holes unique; their Schwartzchild radius is outside their physical radius because their mass is compressed into such a tiny space.
Because the outer edge of the event horizon is the last point at which light can escape it also marks the last point at which events can be seen by distant observers. Anything past this point can never be observed.
The reason the Schwarzschild radius is called a ‘coordinate singularity’ is that it can be removed with a clever choice of coordinate system. The second singularity can’t be dealt with in this way. This makes it the ‘true’ physical singularity of the black hole itself.
This is known as the gravitational singularity and is found at the centre of the black hole (r=0). This is the end-point for every particle that falls into a black hole. It’s also the point the Einstein field equations break down… maybe even all the laws of physics themselves.
The fact that the escape velocity of the event horizon exceeds the speed of light means that no physical signal could ever carry information from the central singularity to distant observers. We are forever sealed off from this aspect of black holes, which will therefore forever remain in the domain of theory.
How to Make a Black Hole
We’ve already seen that for a body with the mass of Earth to become a black hole, its diameter would have to shrink to less than 2cm. This is obviously something that just isn’t possible. In fact, not even our Sun has enough mass to end its life as a black hole. Only stars with around three times the mass of the Sun are massive enough to end their lives in this way.
But why is that the case?
It won’t surprise you to learn that for an astronomical body to become a black hole it must meet and exceed a series of limits. These limits are created by outward forces that are resisting against the inward force that leads to gravitational collapse.
For planets and other bodies with relatively small masses, the electromagnetic repulsion between atoms is strong enough to grant them stability against total gravitational collapse. For large stars the situation is different.
During the main life cycle of stars–the period of the fusion of hydrogen atoms to helium atoms–the primary protection against gravitational collapse is the outward thermal and radiation pressures that are generated by these nuclear processes. That means that the first wave of gravitational collapse occurs when a star’s hydrogen fuel is exhausted and inward pressure can no longer be resisted.
Should a star have enough mass, this collapse forces together atoms in the nucleus enough to reignite nuclear fusion— with helium atoms now fusing to create heavier elements. When this helium is exhausted, the process happens again, with the collapse again stalling if there is enough pressure to trigger the fusion of heavier elements still.
Stars like the Sun will eventually reach the point where their mass is no longer sufficient to kick start the nuclear burning of increasingly heavier elements. But if it isn’t nuclear fusion that is generating the outward forces that prevent complete collapse, what is preventing these lower-mass stars from becoming black holes?
Placing Limits on Gravitational Collapse
Lower-mass stars like the Sun will end their lives as white dwarf stars with a black hole form out of reach. The mechanism protecting these white dwarfs against complete collapse is a quantum mechanical phenomenon called degeneracy.
This ‘degeneracy pressure’ is a factor of the Pauli exclusion principle, which states that certain particles– known as fermions, which include electrons, protons, and neutrons– are forbidden from occupying the same ‘quantum states.’ This means that they resist being tightly crammed together.
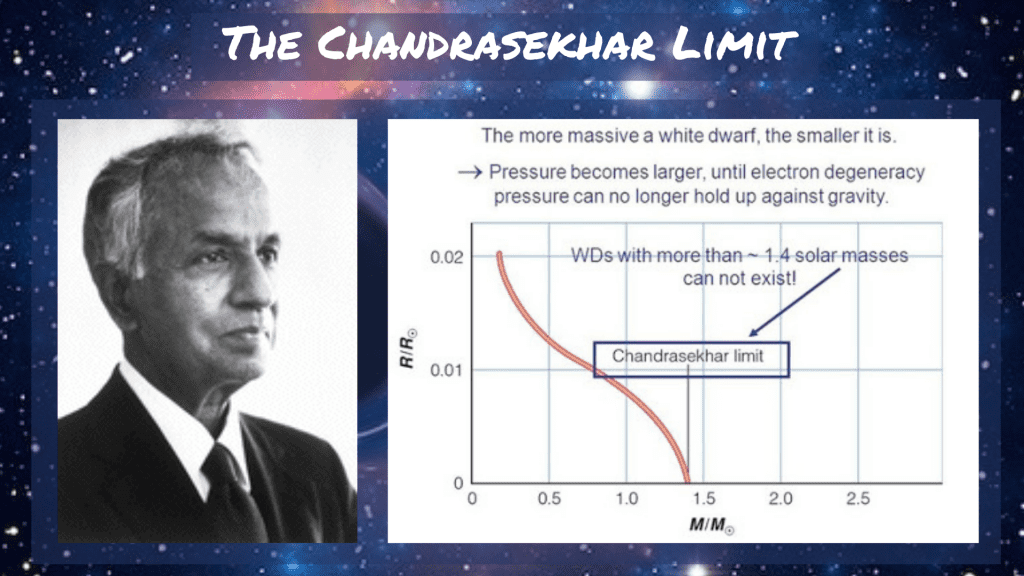
This theory and the limitation it introduced led Indian-American astrophysicist Subrahmanyan Chandrasekhar to question if there was an upper cap at which this protection against gravitational collapse would fail.
Chandrasekhar –awarded the 1983 Nobel Prize in physics for his work concerning stellar evolution– proposed in 1931 that above 1.4 solar masses, a white dwarf would no longer be protected from gravitational collapse by degeneracy pressure. Past this limit — termed the Chandrasekhar limit — gravity overwhelms the Pauli exclusion principle and gravitational collapse can continue.
But there is another limit that prevents stars of even this greater mass from creating black holes.
Thanks to the 1932 discovery of neutrons — the neutral partner of protons in atomic nuclei — Russian theoretical physicist Lev Landau began to ponder the possible existence of neutron stars. The outer part of these stars would contain neutron-rich nuclei, whilst the inner sections would be formed from a ‘quantum fluid’ comprised of mostly neutrons
These neutron stars would also be protected against gravitational collapse by degeneracy pressure — this time provided by this neutron fluid. In addition to this, the greater mass of the neutron in comparison to the electron would allow neutron stars to reach a greater density before undergoing collapse.
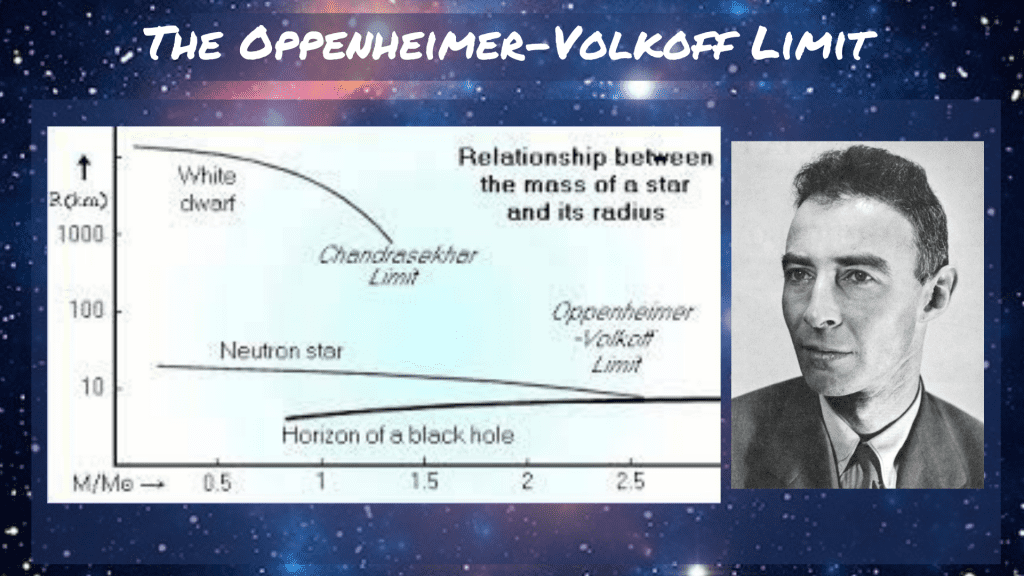
By 1939, Robert Oppenheimer had calculated that the mass-limit for neutron stars would be roughly 3 times the mass of the Sun.
To put this into perspective, a white dwarf with the mass of the Sun would be expected to have a millionth of our star’s volume — giving it a radius of 5000km, roughly that of the Earth. A neutron star of a similar mass though would have a radius of about 20km — roughly the size of a city.
Above the Oppenheimer-Volkoff limit, gravitational collapse begins again. This time no limits exist between this collapse and the creation of the densest possible state in which matter can exist. The state found at the central singularity of a black hole.
We’ve covered the creation of black holes and the hurdles that stand in the way of the formation of such areas of spacetime, but theory isn’t quite ready to hand black holes over to practical observations just yet. The field equations of general relativity can also be useful in the categorisation of black holes.
The four types of black holes
Categorising black holes is actually fairly straight-forward thanks to the fact that they possess very few independent qualities. John Wheeler had a colourful way of describing this lack of characteristics. The physicist once commented that black holes ‘have no hair,’ meaning that outside a few characteristics they are essentially indistinguishable. This comment became immortalised as the no-hair theorem of black holes.
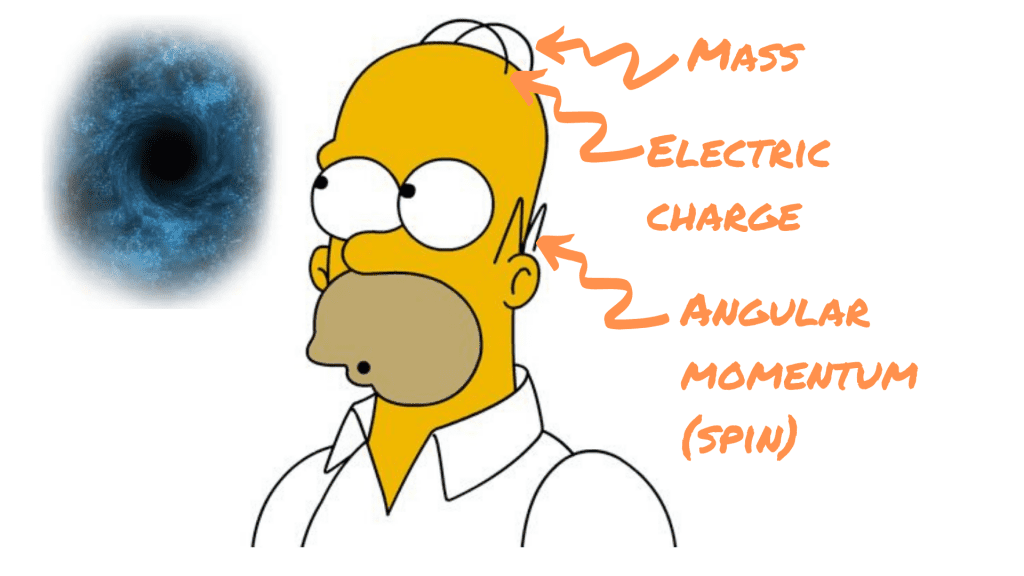
Black holes have only three independent measurable properties — mass, angular momentum and electric charge. All black holes must have mass, so this means there are only four different types of a black hole based on these qualities. Each is defined by the metric or the function used to describe it.
This means that black holes can be quite easily catagorised by the properties they possess as seen below.
This isn’t the most common or most suitable method of categorising black holes, however. As mass is the only property that is common to all black holes, the most straight-forward and natural way of listing them is by their mass. These mass categories are imperfectly defined and so far black holes in some of the categories–most notably intermediate black holes– remain undetected.

Cosmologists believe that the majority of black holes are rotating and non-charged Kerr black holes. And the study of these spacetime events reveals a phenomenon that perfectly exemplifies their power and influence on spacetime.
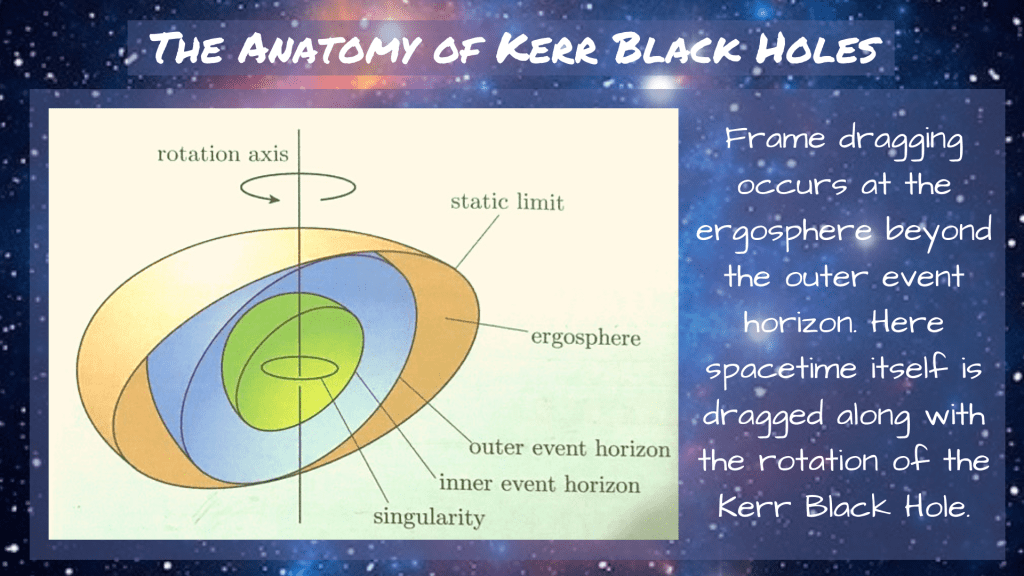
The Anatomy of a Kerr Black Hole
The mathematics of the Kerr metric used to describe non-charged rotating black holes reveals that as they rotate, the very fabric of spacetime that surrounds them is dragged along in the direction of the rotation.
The powerful phenomenon is known as ‘frame-dragging’ or the Lense-Thirring effect and leads to the violent churning environments that surround Kerr black holes. Recent research has revealed that this frame-dragging could be responsible for the breaking and reconnecting of magnetic field lines that in-turn, launch powerful astrophysical jets into the cosmos.
The static limit of a Kerr black hole also has an interesting physical significance. This is the point at which light–or any particle for that matter– is no-longer free to travel in any direction. Though not a light-trapping surface like the event horizon, the static limit pulls light in the direction of rotation of the black hole. Thus, light can still escape the static limit but only in a specific direction.
British theoretical physicist and 2020 Nobel Laureate Sir Roger Penrose also suggested that the static limit could be responsible for a process that could cause black holes to ‘leak’ energy into the surrounding Universe. Should a particle decay into a particle and its corresponding anti-particle at the edge of the static limit it would be possible for the latter to fall into the black hole, whilst its counterpart is launched into the surrounding Universe.
This has the net effect of reducing the black hole’s mass whilst increasing the mass content of the wider Universe.
We’ve seen what happens to light at the edge of a black hole and explored the fate of particles that fall within a Kerr black hole’s static limit, but what would happen to an astronaut that strayed too close to the edge of such a spacetime event?
Death by Spaghettification
Of course, any astronaut falling into a black hole would be completely crushed upon reaching its central gravitational singularity, but the journey may spell doom even before this point has been reached. This is thanks to the tidal forces generated by the black hole’s immense gravitational influence.
As the astronaut’s centre of mass falls towards the black hole, the object’s effect on spacetime around it causes their head and feet to arrive at significantly different times. The difference in the gravitational force at the astronaut’s head and feet gives rise to such a huge tidal force that means their body would be simultaneously compressed at the sides and stretched out.
Physicists refer to this process as spaghettification. A witty name for a pretty horrible way to die. Fortunately, we haven’t yet lost any astronauts to this bizarre demise, but astronomers have been able to watch stars meet the same fate.
For a stellar-mass black hole, spaghettification would occur not just before our astronaut reaches the central singularity, but also well before they even hit the event horizon. For a black hole 40 times the mass of our Sun — spaghettification would occur at about 1,000 km out from the event horizon, which is, itself, 120 km from the central gravitational singularity.
As well as developing the Oppenheimer-Volkoff limit, Oppenheimer also used general relativity to describe how a total gravitational collapse should appear to a distant observer. They would consider the collapse to take an infinitely long time, the process appearing to slow and freeze as the star’s surface shrinks towards the Schwarzschild radius.
An astronaut falling into a black hole would be immortalized in a similar way to a distant observer, though they themselves–could they have survived spaghettification– they would notice nothing. The passing of Rs would just seem a natural part of the fall to them despite it marking the point of no return.
Much More to Learn…
After emerging from the mathematics of general relativity at the earlier stages of the 20th Century, black holes have developed from a theoretical curiosity to the status of scientific reality. In the process, they have indelibly worked their way into our culture and lexicon.

Perhaps the most exciting thing about black holes is that there is so much we don’t yet know about them. As a striking example of that, almost all the information listed above resulted just from theory and the interrogation of the maths of Einstein’s field equations.
Unlocking the secrets held by black holes could, in turn, reveal how galaxies evolve and how the Universe itself has changed since its early epochs.
Sources and Further Reading
Relativity, Gravitation and Cosmology, Robert J. Lambourne, Cambridge Press, [2010].
Relativity, Gravitation and Cosmology: A basic introduction, Ta-Pei Cheng, Oxford University Press, [2005].
Extreme Environment Astrophysics, Ulrich Kolb, Cambridge Press, [2010].
Stellar Evolution and Nucleosynthesis, Sean G. Ryan, Andrew J. Norton, Cambridge Press, [2010].
Cosmology, Matts Roos, Wiley Publishing, [2003].
Was this helpful?