In a series of papers beginning in 1905 Einstein’s theory of special relativity revolutionized the concepts of space and time, uniting them into a single entity–spacetime. But, the most famous element of special relativity–as famous as the man himself–was absent from the first paper.
Mass-energy equivalence, represented by E=mc2, would be introduced in a later paper published in November 1905. And just as Einstein had already unified space and time–this paper would unite energy and mass.
So what does the mass-energy equivalence tell us and what is the equation E=mc2 saying about the Universe?
The Basics
If you wanted to walk away from this article with one piece of information about the equation E=mc2 (and I hope you won’t) what would that be?
Essentially the simplified version of the equation of special relativity tells us that mass and energy are different forms of the same thing– mass is a form of energy. Probably the second most important piece of information to take away is the fact that these two aspects of the Universe are interchangeable, and the mitigating factor is the speed of light squared.
Still with us? Good!
Perhaps the most surprising thing about the equation E=mc2 is how deceptively simple it is for something so profound. Especially when considering that as the equation that describes how stars release energy and thus make all life possible. Mathematical formulae don’t get much more foundational.
Gathering Momentum: Where Does the Mass-Energy Equivalence Come From?
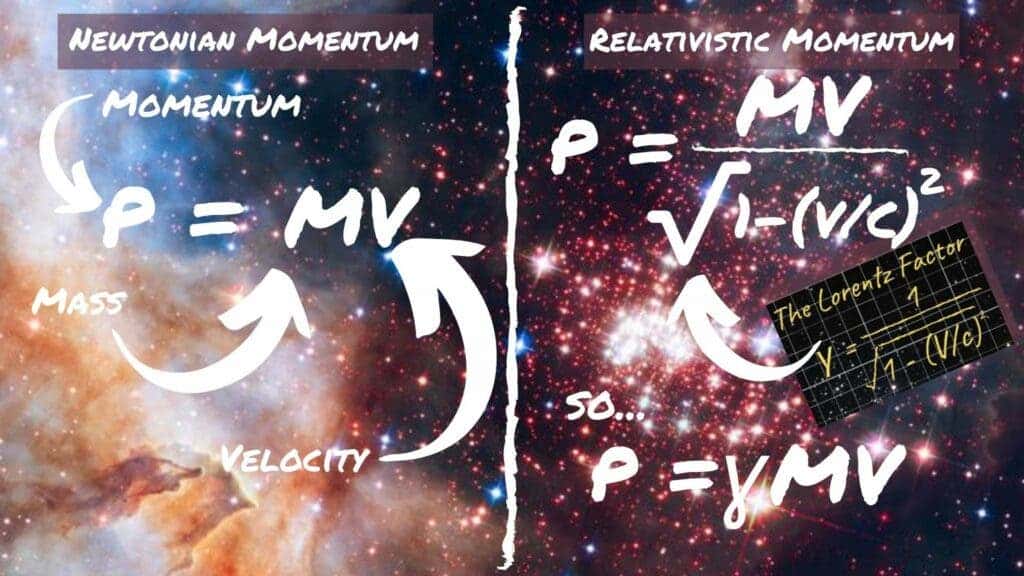
There are actually a few ways of considering the origin of E=mc2. One way is by considering how the relationship it describes can emerge when comparing the relativistic equation for momentum and its Newtonian counterpart. The major difference between the two, as you’ll see below, is multiplication by the Lorentz factor — you might remember in the last part of this guide to special relativity —concerning space and time— I told you it gets everywhere in special relativity!
Whilst you could argue that the only difference between the two is that velocity (v) has been replaced with a more complex counterpart that approaches v when speeds are far less than light–everyday speeds that we see everyday objects around us move at–but some physicists find this more significant than a mere substitution.
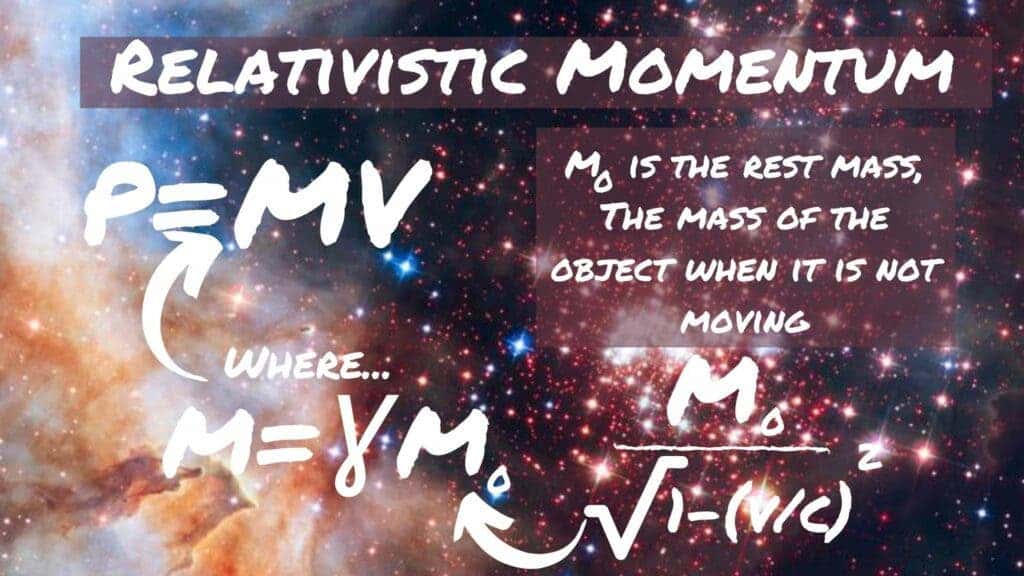
These scientists would argue that this new factor ‘belongs’ to the mass of the system in question. This view means that mass increases as velocity increases, and this means there is a discernable difference between an object’s ‘moving mass’ and its ‘rest mass.’
So, let’s look at that equation for momentum again with the idea of rest mass included.
So, if mass is increasing as velocity increases, what is responsible for this rise?
Let’s conduct an experiment to find out. Our lab bench is the 2-mile long linear particle accelerator at SLAC National Laboratory, California. Using powerful electromagnetic forces, we take electrons and accelerate them to near the speed of light. When the electrons emerge at the other end of the accelerator we find that their relativistic mass has increased by a staggering factor of 40,000.
As the electrons slow, they lose this mass again. Thus, we can see it’s the addition of kinetic energy to the object that is increasing its mass. That gives us a good hint that energy and mass are interconnected.
But, this conclusion leads to an interesting question; if the energy of motion is associated with an object’s mass when it is moving, is there energy associated with the object’s mass when it is at rest, and what kind of energy could this be?
Locked-Up Energy
An object at rest without kinetic energy can, with the transformation of an infinitesimally small amount of mass, provide energy enough to power the stars.
As the equation E=mc2 and the fact that the speed of light squared is an extremely large number implies, in terms of energy just a little mass goes a very long way. To demonstrate this, let’s see how much energy would be released if you could completely transform the rest mass of a single grain of sugar.
That’s a lot of energy!
In fact, it is roughly equivalent to the amount of energy released by ‘little boy’– the nuclear fission bomb that devastated Hiroshima on the 6th August 1945.
That means that even when an object is at standstill it has energy associated with it. A lot of energy.
As you might have guessed by this point, as energy and mass are closely associated and there are many forms of energy there are also many ways to give an object increased mass. Heating a metal rod, for example, increases the rod’s mass, but by such a small amount that it goes unnoticed. Just as liberating a tiny bit of mass releases a tremendous amount of energy, adding a relatively small amount of heat energy results in an insignificant mass increase.
We’ve already seeen that we can accelerate a particle and increase its relativistic mass, but is there anything we can do to increase a system’s rest mass?
E=mc2: Breaking the Law (and Billiard Balls)!
Until the advent of special relativity two laws, in particular, had governed the field of physics when it comes to collisions, explosions, and all that cool violent stuff: the conservation of mass and the conservation of energy. Special relativity challenged this, suggesting instead that it is not mass or energy that is conserved, but the total relativistic energy of the system.
Let’s do another experiment to test these ideas… The first location we’ll travel to in order to do this… a billiard table at the Dog & Duck pub, London.

At the billiard table, we strike a billiard ball 0.17 kg toward a stationary billiard ball of the same mass at around 2 metres per second. We hit the ball perfectly straight on so that all of the kinetic energy of the first ball is transferred to the second ball.
If we could measure the kinetic energy of the initial ball, then measure the kinetic energy of both balls after the collision, we would find that–accounting for the small losses of energy to heat and sound–the total energy of the system after the collision is the same as the energy before the collision.
That’s the conservation of energy.
Let’s rerun that experiment again, but this time we launch the billard ball so hard that instead of knocking the target ball across the table, it shatters it. Collecting together the fragments of the shattered ball and remeasuring the mass of the system, we would find the final mass is exactly the same as the initial mass.
And that’s the conservation of mass.
We’re starting to get funny looks from the Dog & Duck regulars now, and the landlord looks angry about the destruction of one of his billiard balls. Luckily, the third part of our test requires we relocate to CERN, Geneva. So we down our drinks, grab our coats and hurry out the door.
Trying the experiment a third time, we are going to replace the billiard table with the Large Hadron Collider (LHC)–that’s some upgrade– and the billiard balls with electrons and their equal rest mass anti-particles– positrons.
Using powerful magnets to feed these fundamental particles with kinetic energy we accelerate them to near light speed, directing them towards each other and colliding them. The result is a shower of particles that previously weren’t present. But, unlike in our billiard ball example, when we measure the rest mass of the system it has not remained the same.
Just one of the particles we observe after the collision event is a neutral pion–a particle with a rest mass 264 times the rest mass of an electron and thus 132 times the initial rest mass we began with.
Clearly, the creation of this pion has taken some of the kinetic energy we poured into the electrons and converted it to rest mass. We watch as the pion decays into a muon with a rest mass 204 times that of an electron, and this decays into particles that are lighter still. Each time the decay releases energy in the form of pulses of light.
Relativistic Energy .vs Rest Energy
By now it is probably clear that in special relativity rest mass and relativistic mass are very different concepts, which means that it shouldn’t come as too much of a surprise that rest energy and relativistic energy are also separate things.
Let’s alter that initial infographic to reflect the fact that the equation E=mc2 actually describes rest energy.
This raises the questions (if I’m doing this right that is) what is the equation for relativistic energy?
It’s time for another non-surprise. The equation for relativistic energy is just the equation for rest energy with that Lorentz factor playing a role.
Ultimately, it is this relativistic energy that is conserved, thus whilst we’ve sacrificed earlier ideas of the conservation of mass and the conservation of energy, we’ve recovered a relativistic version of those laws.
Of course, the presence of that Lorentz factor tells us that when speeds are nowhere near that of light — everyday speeds like that of the billiard balls in the Dog & Duck–the laws of conservation of mass and energy are sufficeint to describe these low-energy systems.
The Consequences of E=mc2
It’s hard to talk about the energy-mass equivalence or E=mc2 without touching upon the nuclear weapons that devasted Hiroshima and Nagasaki at the close of the Second World War.
It’s an unfortunate and cruel irony that Einstein–a man who was a staunch pacifist during his lifetime–has his name eternally connected to the ultimate embodiment of the most destructive elements of human nature.

Nuclear radiation had been discovered at least a decade before Einstein unveiled special relativity, but scientists had struggled to explain exactly where that energy was coming from.
That is because as rearranging E=mc2 implies, a small release of energy would be the result of the loss of an almost infinitesimally small amount of rest mass –certainly immeasurable at the time of discovery.
Of course, as we mention above, we now understand that small conversion of rest mass into energy to be the phenomena that power the stars. Every second, our own star–the Sun– takes roughly 600 tonnes of hydrogen and converts it to 596 tonnes of helium, releasing the difference in rest mass between the two as around 4 x 1026 Joules of energy.
We’ve also harnessed the mass-energy equivalence to power our homes via nuclear power plants, as well as using it to unleash a terrifying embodiment of death and destruction into our collective imaginations.
We could probably ruminate more about special relativity and its elements, as its importance to modern physics simply cannot be overstated. But, Einstein wasn’t done.
Thinking about spacetime, energy and mass had open a door and started Einstein on an intellectual journey that would take a decade to complete.
The great physicist saw special relativity as a great theory to explain physics in an empty region of space, but what if that region is occupied by a planet or a star? In those ‘general’ circumstances, a new theory would be needed. And in 1915, this need would lead Einstein to his greatest and most inspirational theory–the geometric theory of gravity, better known as general relativity.
Sources and Further Reading
Stannard. R., ‘Relativity: A Short Introduction,’ Oxford University Press, [2008].
Lambourne. R. J., ‘Relativity, Gravitation and Cosmology,’ Cambridge University Press, [2010].
Cheng. T-P., ‘Relativity, Gravitation and Cosmology,’ Oxford University Press, [2005].
Fischer. K., ‘Relativity for Everyone,’ Springer, [2015].
Takeuchi. T., ‘An Illustrated Guide to Relativity,’ Cambridge University Press, [2010].