Math can be tough and complicated. It’s also the foundation of our modern society, and while it may not always seem like this, it can also be interesting. Perhaps if we look at it in a different light, we could see it differently. A more meme-y light, that is.

Starting off easy, 2’s go well together, whether it’s addition, exponential, or multiplication. But when when it comes to 3’s, it’s not a party. Oh, and don’t even get started with the 0’s.

Zero to the power of zero has been the bane of many mathematicians across the years — and many students at that. They play an important role in limits. Speaking of that, how well do you know your limits?

If you don’t get this joke, it’s actually a variation of one of Zeno’s paradoxes. Zeno’s paradoxes have been debated for centuries, and while the advent of analysis has offered some tools to solve them with, they’re still important food for thought.
If this doesn’t work for you, let’s get to something simpler.

Nothing like a simple factorial joke to get the guys smiling, right?
Or maybe you prefer a good root joke.

Hopefully, if you don’t get the one above, you need to square up. Oh, and you might really hate the next few ones, cause we’re about to dive into some integral parts of mathematics.
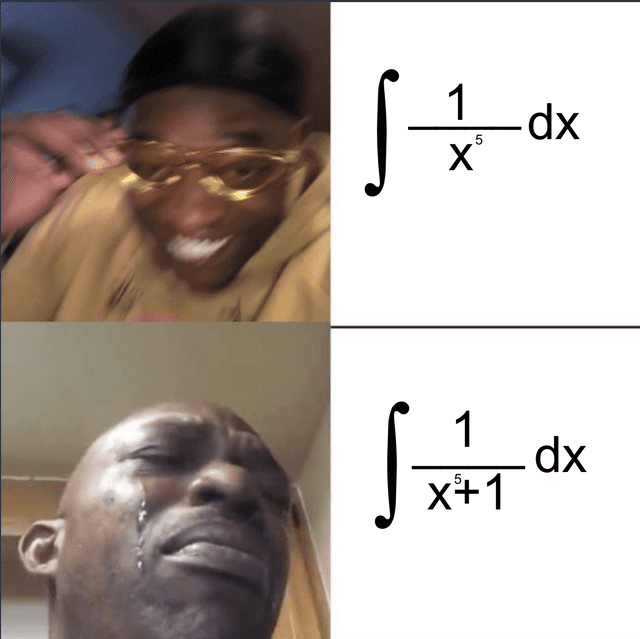
Seriously, how can a single ‘1’ make such a big difference — and make so many highschoolers and university students cry?

Seriously, this ∫ has made so many of us cry. Integrals are hard.

Derivatives are also pretty hard, but they don’t affect everyone. In particular, they don’t affect ex — of course, in this case, e is Euler’s number, a mathematical constant approximately equal to 2.71828, and the base of natural logarithms. The derivative of ex is ex and the number is not affected by derivation.

This one should have probably followed the other integral ones, but it’s hard to stomach too many integral memes in a row. Yet again, another one to make students cry — forgetting the “plus C”.

Not everything is integration, thank God, some things are as simple as a simple plot.
Did I mention how common it is to forget the constant of integration (the “plus C”) in integrals?

Oftentimes, mathematics can seem abstract, but other times, it gets very concrete. Like here:

Here’s one that will make Pythagoras fans cry — an impossible triangle with the sides of 0, 1, and the complex number i. By the way, can you tell why this triangle doesn’t make sense?
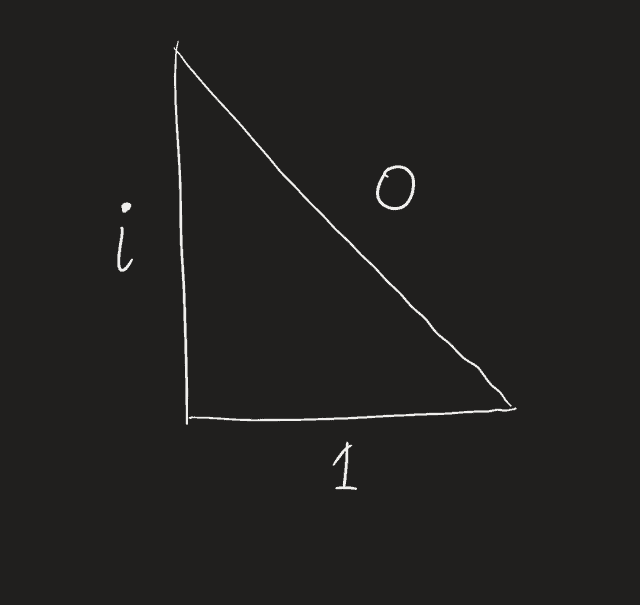
If you thought that triangle was wrong, well, wait ’til you see how we can extrapolate absurd things.

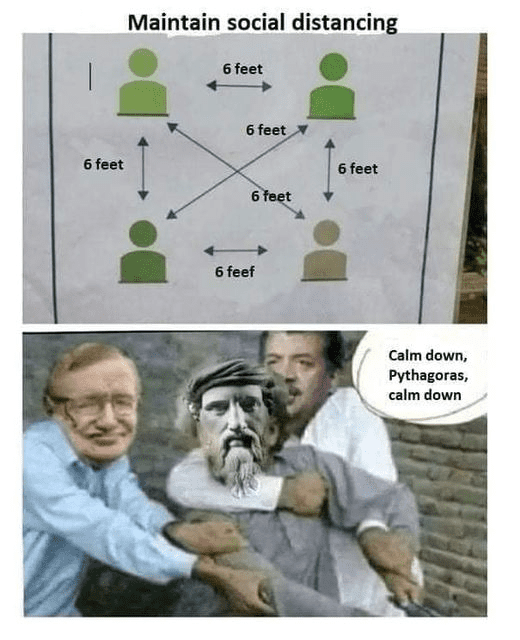
For some reason, Pythagoras’ theory is hard to get, making social distancing very difficult geometrically.
Lastly, let’s end with another derivative meme. You’re never changing ex, you derivative girl.

Was this helpful?



