Given that space is tridimensional, it can seem odd that many cosmic objects arrange themselves in the same plane. Take our solar system for instance, where the planets orbit the sun in the same plane instead of being distributed in a spherical configuration. This holds true on both small and astronomical scales. Saturn’s rings are arranged in a disc shape in the same plane with the planet’s center of mass. Asteroid belts are also flat and so are most galaxies.
In short, this pattern can be explained by a fundamental law of physics: the conservation of angular momentum. Angular momentum is the rotational analog of linear momentum and is defined as the product of its moment of inertia and its angular velocity.
The law of conservation of angular momentum
The law of conservation of angular momentum states that when no external torque acts on an object, no change of angular momentum will occur. If the net torque is zero, then angular momentum is constant or conserved.
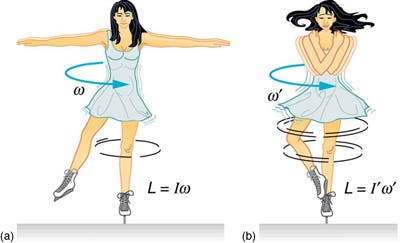
It’s the conservation of angular momentum that can explain why an ice skater can increase the angular acceleration by bringing her arms and legs close to the vertical axis of rotation. Because the moment is conserved, when the skater decreases the rotational inertia, the rotation rate must increase.
Credit: Boundless.
Why the solar system is (almost) flat
Credit: NASA/JPL.
How does all this relate to the flatness of the solar system more exactly? Some 4.6 billion years ago, there was no planet Earth and the Sun had yet to form. Instead, a huge blob of gas and dust floated about for millions of square miles.
Attracted by gravity, particles of matter gradually moved closer eventually resulting in collisions. Whenever some particles collide, their new trajectories are random but although the new direction is impossible to predict the angular momentum must remain constant in an isolated system because the local gravitational effect of other bodies is negligible.
The angular momentum is a physical quantity that’s constant around a fixed axis, which is a point in a 2-D space and line in 3-D space. This means the system rotates along a plane that’s perpendicular to this axis. In our particular case, the solar system, this means that when all that primordial gas and dust started to collide, the particles could move in any direction but all the up and down motions phased each other out. In time, the particles lose their freedom to move across all planes except a select 2D plane.
Because all that matter formed a disk, all in a plane, all of the planets formed in a plane as well. Were it not for the law of conservation of angular momentum, it would have been impossible for stars and planets to form. Our very existence is tied to this fundamental law of physics.
As a caveat, we must note that the solar system isn’t perfectly flat. Pluto, the dwarf planet, has an orbital inclination of about 17 degrees relative to the plane of the solar system and right at the center of nearly all galaxies lies a large bulge although 98% of the stars in a galaxy orbit inside spiral arm filaments around the center of the galaxy. Aside from these oddities, the solar system is pretty tidily arranged in the same plane.
Other solar systems can be even flatter. In a study published The Monthly Notices of the Royal Astronomical Society, scientists modeled the solar systems detected by the Kepler Space Telescope and found most of these are shaped like our solar system. Even the now famous TRAPPIST-1 planetary system, which has 7-Earth like planet only 39 light-years away, is almost perfectly flat.
“The wealth of the Kepler planet data allows for the first time detailed studies of planet systems outside the solar system. We are now able to ask and answer questions like, how common are planet systems like our own?” Tim Bovaird, a researcher at ANU the lead author of the new study, said in a press release.
