
Pi or π is the ratio between a circle’s circumference and diameter. It doesn’t matter how big or small the circle is – the ratio stays the same, and the constant has proven to be indispensable for mathematicians. Along the ages, computing pi – an irrational number, hence its decimal representation never ends (supercomputers managed to calculate trillions of digits for pi) – has proven to be both an entertaining and head banging quest for mathematicians. The first calculation of pi was done by Archimedes of Syracuse (287–212 BC), one of the greatest mathematicians of the ancient world. Archimedes bracketed a circle with polygons, which allowed him to break the circle into squares. Using Pythagoras’ theorem and the perimeter of a square, both known to Archimedes, the Greek savant used this trick with 96 sided polygons to correctly estimate Pi to about two digits (3.14), proving 3.1408 < Pi < 3.1428.
Until the advent of calculus and computing infinite series, not that many digits were added to the ones found by Archimedes for more than a 1,500 years. One major breakthrough was made in 1655 when the English mathematician derived a formula for pi as the product of an infinite series of ratios. Oddly enough, but not that surprising considering the prevalence of pi in nature, researchers from the University of Rochester reached the same formula while they were computing the quantum mechanical energy stats of hydrogen.
In quantum mechanics, a technique called the variational approach can be used to approximate the energy states of quantum systems, like molecules, that can’t be solved exactly. Carl Hagen, a particle physicist at the University of Rochester, made a habit out of teaching the technique to his students by applying it to hydrogen. The thing about the hydrogen atom is that its energy levels can be computed directly using the quantum calculations developed by Danish physicist Niels Bohr in the early twentieth century. By applying the variational approach and then comparing the result to the exact solution, students could calculate the error in the approximation. But after Hagen himself started solving the problem, he noticed a peculiar trend: the error of the variational approach was about 15 percent for the ground state of hydrogen, 10 percent for the first excited state, and kept getting smaller as the excited states grew larger.

Hagen needed some backup, so he recruited mathematician Tamar Friedmann to help out. The two found that the ratio yielded—effectively—the Wallis formula for π.
Specifically, the calculation of Friedmann and Hagen resulted in an expression involving special mathematical functions called gamma functions leading to the formula
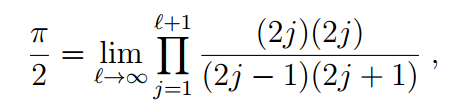
which can be reduced to the classic Wallis formula.
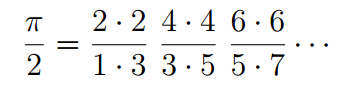
“We didn’t just find pi,” said Friedmann, a visiting assistant professor of mathematics and a research associate of high energy physics, and co-author of a paper published this week in the Journal of Mathematical Physics. “We found the classic seventeenth century Wallis formula for pi, making us the first to derive it from physics, in general, and quantum mechanics, in particular.”
“The value of pi has taken on a mythical status, in part, because it’s impossible to write it down with 100 percent accuracy,” said Friedmann, “It cannot even be accurately expressed as a ratio of integers, and is, instead, best represented as a formula.”
It’s amazing to see pi pop up in such a natural way, with no circles involved what so ever. And how elegant to find this connection by reaching the same results as a XVIIth century mathematician.
“This derivation of pi is a surprise of the familiar, much like a magician’s trick,” said Moshe Machover of King’s College London, who was not involved in the study. “A child who sees a trick done for the first time may be only surprised. But an adult, who has seen numerous tricks over the years, experiences both surprise and familiarity.”
“Nature had kept this secret for the last 80 years,” Friedmann said. “I’m glad we revealed it.”
Was this helpful?



