How big is a petabyte, exabyte or yottabyte? Let’s look at the largest units of data storage

Thirty years ago, the biggest hard drives stored about 10MB of data. That’s barely enough to store two or three .mp3 tracks. Now, a typical notebook has one terabyte of storage or nearly 100,000 times more but even this figure is laughable when you consider how much data we’re generating today on a daily basis. According to IBM, every day we’re creating 2.5 quintillion bytes of data, enough to fill 125,00 DVDs, and 90% of today’s digital data was created in the last two years.

Even those who are computer savvy still look at data at the gigabyte or terabyte-scale but it’s clear we’re moving well past this point. Navigating the different units of data storage can be confusing and dizzying so let’s take a brief overview of how we quantify data and put some context on some of the more obscure units of digital information like the petabyte or yottabyte.

Units of data

The bit

The bit, short for BInary digiT, is the smallest unit of data a computer can read. Simply put, it can be either a 1 or 0.

The Byte

The byte is composed of eight bits.

• 0.1 bytes: a binary decision
• 1 byte: a single character
• 10 bytes: a single word
• 100 bytes: a telegram OR A punched card

Kilobyte (1024 Bytes)

• 1 Kilobyte: a very short story
• 2 Kilobytes: a typewritten page
• 10 Kilobytes: an encyclopaedic page or a deck of punched cards
• 50 Kilobytes: a compressed document image page
• 100 Kilobytes: a low-resolution photograph
• 200 Kilobytes: a box of punched cards
• 500 Kilobytes: a very heavy box of punched cards

Megabyte (1024 Kilobytes)

• 1 Megabyte: 4 books (873 pages of plain text) ora a 3.5-inch floppy disk
• 2 Megabytes: a high-resolution photograph
• 5 Megabytes: the complete works of Shakespeare or 30 seconds of TV-quality video
• 10 Megabytes: a minute of high-fidelity sound or a digital chest X-ray
• 20 Megabytes: a box of floppy disks
• 50 Megabytes: a digital mammogram
• 100 Megabytes: 1 meter of shelved books or a two-volume encyclopedic book
• 200 Megabytes: a reel of 9-track tape or an IBM 3480 cartridge tape
• 500 Megabytes: a CD-ROM

Gigabyte (1,024 Megabytes, or 1,048,576 Kilobytes)

• 1 Gigabyte: a pickup truck filled with paper or a symphony in high-fidelity sound or a movie at TV quality. 1 Gigabyte could hold the contents of about 10 yards of books on a shelf.
• 2 Gigabytes: 20 meters of shelved books
• 5 Gigabytes: an 8mm Exabyte tape
• 20 Gigabytes: a high-quality audio collection of the works of Beethoven or a VHS tape used for digital data
• 50 Gigabytes: a floor of books or hundreds of 9-track tapes
• 100 Gigabytes: a floor of academic journals

Terabyte (1,024 Gigabytes)

• 1 Terabyte: An automated tape robot or all the X-ray films in a large technological hospital or 50,000 trees made into paper and printed.
• 1 Terabyte: 1,613 650MB CDs or 4,581,298 books.
• 1 Terabyte: 1,000 copies of the Encyclopedia Britannica.
• 2 Terabytes: an academic research library or a cabinet full of Exabyte tapes
• 10 Terabytes: the printed collection of the US Library of Congress

Petabyte  (1,024 Terabytes, or 1,048,576 Gigabytes)

• 1 Petabyte: 5 years of Earth Observing System (EOS) (at 46 mbps)
• 1 Petabyte: 20 million 4-door filing cabinets full of text or 500 billion pages of standard printed text.
• 2 Petabytes: all US academic research libraries.
• 20 Petabytes: production of hard-disk drives in 1995
• 200 Petabytes: all printed material ever OR Production of digital magnetic tape in 1995

Exabyte (1,024 Petabytes)

• An exabyte of data was created on the Internet each day in 2012 or 250 million DVDs worth of information.
• 5 Exabytes: All words ever spoken by all the human beings who lived in history.

Zettabyte (1,024 Exabytes)

• Cisco estimated 1.3 zettabytes of traffic annually over the internet in 2016.

Yottabyte (1,024 Zettabytes, or 1,208,925,819,614,629,174,706,176 bytes)

• It’s equal to one septillion (10²⁴) or, strictly, 2⁸⁰ bytes.
• Its name comes from the prefix ‘Yotta’ derived from the Ancient Greek οκτώ (októ), meaning “eight”, because it is equal to 1,000⁸
• In 2010, it would have cost $100 trillion to make a yottabyte storage system made out of the day’s hard drives.

The ‘Yotta’ prefix was officially introduced in 1991  during a time when it was unimaginable that data could grow any bigger than that. Oh, how wrong we were. To compensate, people have unofficially used their own unsanctioned prefixes like the brontobyte and hellabyte (both are 1,024 yottabytes or 1 followed by 27 zeroes). But since 2022, two new prefixes have been added to the International System of Units, ‘ronna’ (1 followed by 27 zeroes) and ‘quetta’ (1 followed by 30 zeroes).

Ronnabyte (1,024 Exabytes)

• It’s equal to one octillion (10²⁷) bytes.

Quettabyte (1,024 Exabytes)

• It’s equal to one nonillion (10³⁰) bytes.

How digital storage works

Humans perceive information in analog. For instance, what we see or hear is processed in the brain from a continuous stream. In contrast, a mputer is digital and estimates such information using 1s and 0s.

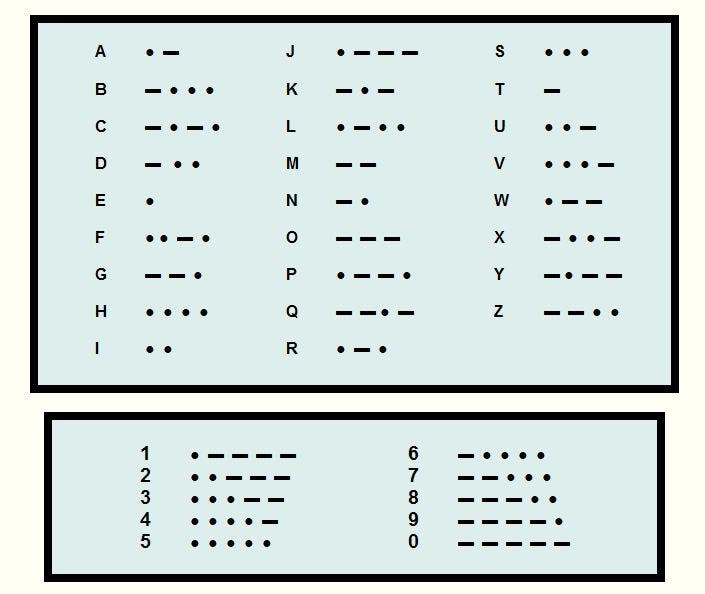
Communicating only in 1s and 0s may sound limiting at first but people have been using sequences of ‘on’ and ‘off’ to transmit messages for a long time. In Victorian times, for instance, people used the telegraph to send ‘dots’ (short signal) or ‘dashes’ (a longer signal) by changing the length of time a switch was on. The person listening on the other end would then decipher the binary data written in Morse code into plain English. Transmitting a message over telegraph could take a while, much longer than a message relayed over the telephone for instance, but in today’s digital age this is not a problem because digital data can be decoded in an instant by computers. In binary, 01100001 could be the number 97, or it could represent the letter ‘a’

Digital storage has several advantages over analog much in the same way digital communication of information holds advantages over analog communication. Perhaps the clearest example of why digital storage is superior to analog is resistance to data corruption. Let’s look at audio or video tapes for a moment. To store data, a thin plastic tape is impregnated with particles of iron oxide which become magnetized or demagnetized in the presence of a magnetic field from an electromagnet coil. Data is then retrieved from the tape by moving it past another coil of wire which magnetizes certain spots around the tape to induce a voltage.

If we were to use analog techniques to store all of our data, like representing a signal by the strength of magnetization of the various spots on the tape, we’d run into a lot of trouble. As the tape ages and magnetization fades, the analog signal will be altered from its original state when the data was first recorded. Moreover, any magnetic field can alter the magnetization on the tape. Since analog signals have infinite resolution, the smallest degree of change will have an impact on the integrity of the data storage.

This is no longer a problem in binary digital form because the strength of magnetization on the tape will be considered in two discrete levels: either ‘high’ or ‘low’. It makes no difference what the in-between states are. Even if the tape experiences slight alterations from magnetic fields, the data is safe from corruption because the discrete levels are still there.