The 2020 Nobel prize in physics has been jointly awarded to Roger Penrose, Reinhart Genzel, and Andrea Ghez for their contributions to our understanding of black holes — the Universe’s most mysterious and compact objects. Whilst Genzel and Ghez claim their share of the most celebrated prize in physics for the discovery of a supermassive compact object at the centre of our galaxy — an object that we would later come to realize was a supermassive black hole which was later named Sagittarius A* (Sgr A*) — Penrose is awarded his share for an arguably more fundamental breakthrough.

The Nobel is awarded to Penrose based on a 1965 paper in which he mathematically demonstrated that black holes arise as a direct consequence of the mathematics of Einstein’s theory of General Relativity. Not only this; but for a body of a certain mass, the collapse into a singularity wasn’t just possible, or even probable. If that collapse could not be halted, singularity formation, Penrose argued, is inevitable.
“For the discovery, that black hole formation is a robust prediction of the general theory of relativity”
The Nobel Commitee awards the 2020 prize in physics to Sir Roger Penrose
The fact that Penrose showed that black holes mathematically emerge from general relativity may seem even more revolutionary when considering that the developer of general relativity — a geometric theory of gravity that suggests mass curves the fabric of spacetime — Albert Einstein did not even believe that black holes actually existed.

It was ten years after Einstein’s death in April 1955 when Penrose showed that singularities form as a result of the mathematics of general relativity and that these singularities act as the ‘heart’ of the black hole. At this central–or gravitational–singularity, Penrose argued, all laws of physics displayed in the outside Universe ceased to apply.
The paper published in January 1965 — just eight years after Penrose earned his Ph.D. from The University of Cambridge — ‘Gravitational Collapse and Spacetime Singularities’ is still widely regarded as the second most important contribution to general relativity after that of Einstein himself.
Yet, Penrose wasn’t the first physicist to mathematically unpick general relativity and discover a singularity. Despite this, his Penrose Singularity Theorem is still considered a watershed moment in the history of general relativity.
Black Holes: A Tale of Two Singularities
“A black hole is to be expected when a large massive body reaches a stage where internal pressure forces are insufficient to hold the body apart against the relentless inward pull of its own gravitational influence.”
Roger Penrose, The Road to Reality
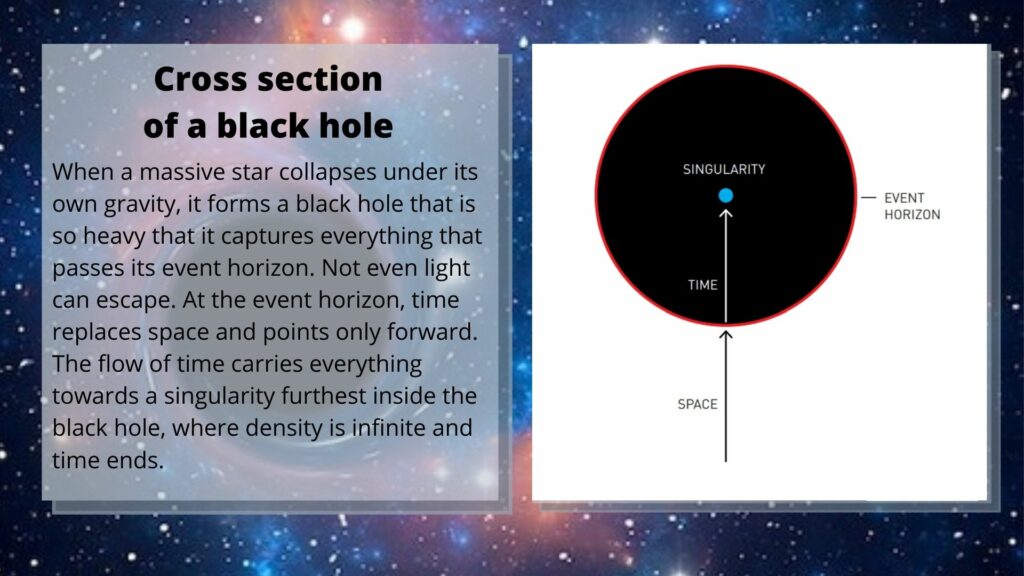
Black holes are generally regarded as possessing two singularities; a coordinate singularity and an ‘actual’ gravitational singularity. Penrose’s work concerned the actual singularity, so named because unlike the coordinate singularity, it could not be removed with a clever choice of coordinate measurement.
That doesn’t mean, however, that the coordinate singularity is unimportant or even easy to dismiss. In fact, you may already be very familiar with the coordinate singularity, albeit under a different name — the event horizon. This boundary marks the point where the region of space defined as a black hole begins, delineating the limit at which light can no longer escape.
The discovery of the event horizon occurred shortly after the first publication of Einstein’s theory of general relativity in 1915. In 1916, whilst serving on the Eastern Front in the First World War astrophysicist Karl Schwarzschild developed the Schwarzschild solution, which described the spacetime geometry of an empty region of space. One of the interesting features of this solution — a coordinate singularity.
The coordinate singularity — also often taking a third more official name as the Schwarzschild radius (Rs) — exists for all massive bodies at r =Rs = 2GM/c². This marks the point where the escape velocity of the body is such that not even light can escape its grasp. For most cosmic bodies the Schwarzschild radius falls well within its own radius (r). For example, the Sun’s Rs occurs at a radius of about 3km from the centre compared to an overall radius of 0.7 million km.
Thus, the Schwarzschild radius or event horizon marks the boundary of a light-trapping surface. A distant observer could see an event taking place at the edge of this surface, but should it pass beyond that boundary — no signal could ever reach our observer. An observer falling with the surface, though, would notice nothing about this boundary.
The passing of Rs would just seem a natural part of the fall to them despite it marking the point of no return. To the distant observer… the surface would freeze and become redder and redder thanks to the phenomena of gravitational redshift — also the reason the event horizon is sometimes referred to as the surface of infinite redshift.
The very definition of a black hole is a massive body whose surface shrinks so much during the gravitational collapse that its surface lies within this boundary. But, what if this collapse continues? When does it reach a central singularity at the heart of the black hole–r= 0 for the mathematically inclined?
Birthing a Black Hole
“We see that the matter continues to collapse inwards through the surface called the event horizon, where the escape velocity indeed becomes the speed of light. Thereafter, no further information from the star itself can reach any outside observer, and a black hole is formed.”
Roger Penrose, The Road to Reality
Penrose and other researchers have found that the equations of general relativity open the possibility that a body may undergo a complete gravitational collapse — shrinking to a point of almost infinite density — and become a black hole.
In order for this to happen, however, a series of limits have to be reached and exceeded. For example, planets are unable to undergo this gravitational collapse as the mass they possess is insufficient to overcome the electromagnetic repulsion between their consistent atoms — thus granting them stability.

Likewise, average-sized stars such as the Sun should also be resistant to gravitational collapse. The plasma found at the centre of stars in this solar-mass range is believed to be roughly ten times the density of lead protecting from complete collapse, whilst the thermal pressure arising from nuclear processes and radiation pressure alone would be sufficient to guarantee a star of low to intermediate-mass stability.
For older, more evolved stars in which nuclear reactions have ceased due to a lack of fuel. It’s a different story. Especially if they have a mass ten times greater than the Sun.
It was suggested as early as the 1920s that small, dense stars — white dwarf stars — were supported against collapse by phenomena arising from quantum mechanics called degeneracy.
This ‘degeneracy pressure’ arises from the Pauli exclusion principle, which states that fermions such as electrons are forbidden from occupying the same ‘quantum state’. This led a physicist called Subrahmanyan Chandrasekhar to question if there was an upper limit to this protection.
In 1931, Chandrasekhar proposed that above 1.4 times the mass of the Sun, a white dwarf would no longer be protected from gravitational collapse by degeneracy pressure. Beyond this boundary— unsurprisingly termed the Chandrasekhar limit — gravity overwhelms the Pauli exclusion principle and gravitational collapse continues unabated.
The discovery of neutrons — the neutral partner of protons in atomic nuclei — in 1932 led Russian theorist Lev Landau to speculate about the possibility of neutron stars. The outer part of these stars would contain neutron-rich nuclei, whilst the inner sections would be formed from a ‘quantum-fluid’ comprised of mostly neutrons.
Again, neutron stars would be protected against gravitational collapse by degeneracy pressure — this time provided by this neutron fluid. In addition to this, the greater mass of the neutron in comparison to the electron would allow neutron stars to reach a greater density before undergoing collapse.
To put this into perspective, a white dwarf with the mass of the Sun would be expected to have a millionth of our star’s volume — giving it a radius of
5000 km roughly that of the Earth. A neutron star of a similar mass though, that would have a radius of about 20km — roughly the size of a city.
By 1939, Robert Oppenheimer had calculated that the mass-limit for neutron stars would be roughly 3 times the mass of the Sun. Above that limit — again, gravitational collapse wins. Oppenheimer also used general relativity to describe how this collapse appears to a distant observer. They would consider the collapse to take an infinitely long time, the process appearing to slow and freeze as the star’s surface shrinks towards the Schwarzschild radius.
Straight to the Heart: The Inevitability of the cental singularity
“So long as Einstein’s picture of classical spacetime can be maintained, acting in accordance with Einstein’s equation then a singularity will be encountered within a black hole. The expectation is that Einstein’s equation will tell us that this singularity cannot be avoided by any matter in the hole…”
Roger Penrose, The Road to Reality
For Penrose, the mathematical proof of a physical singularity at the heart of a black hole arising from this complete collapse was not enough. He wanted to demonstrate the singularity and the effects on a spacetime that would arise there. He did so with the use of ‘light cones’ travelling down a geodesic — an unerringly straight line. In the process, he unveiled the anatomy of the black hole.

A light cone is most simply described as the path that a flash of light created by a single event and travelling in all directions would take through spacetime. Light cones can be especially useful when it comes to physicists calculating which events can be causally linked. If a line can’t be drawn between the two events that fits in the light cone, one cannot have caused the other.
We call a line emerging from a lightcone a ‘world-line’–these move from the central event out through the top of the cone–the future part of the diagram. The worldline shows the possible path of a particle or signal created by the event at the origin of the lightcone. Throwing a light cone at a black hole demonstrates why passing the event horizon means a merger with the central singularity is inevitable.
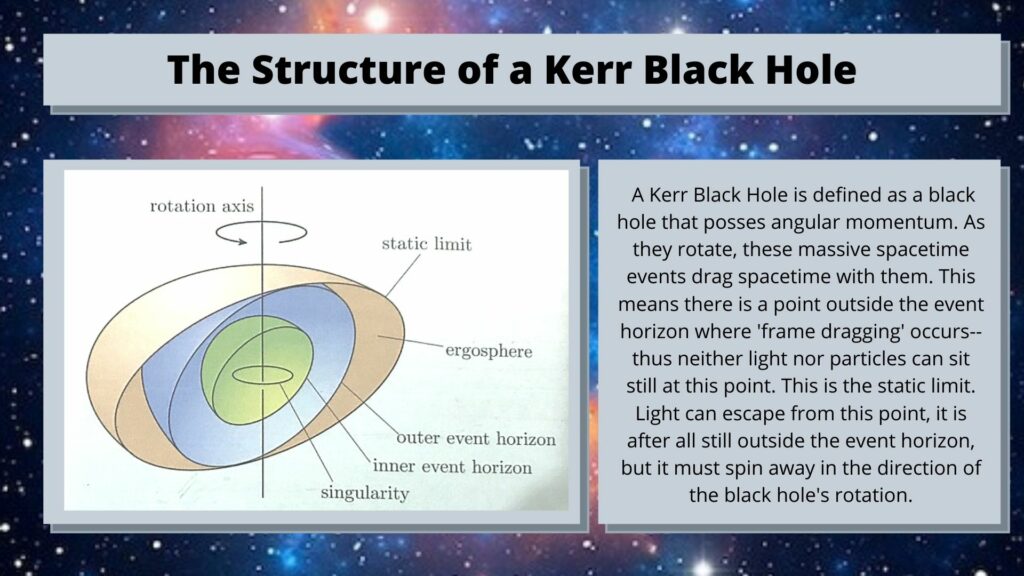
Penrose considered what would happen to a light cone as it approached and passed the event horizon of what is known as a ‘Kerr black hole.’ This is a black hole that is non-charged and rotating. Its angular momentum drags spacetime along with it in an effect researchers call frame dragging.
Far from the black hole, light is free to travel with equal ease in any direction. The lightcones here have a traditionally symmetrical appearance which represents this.
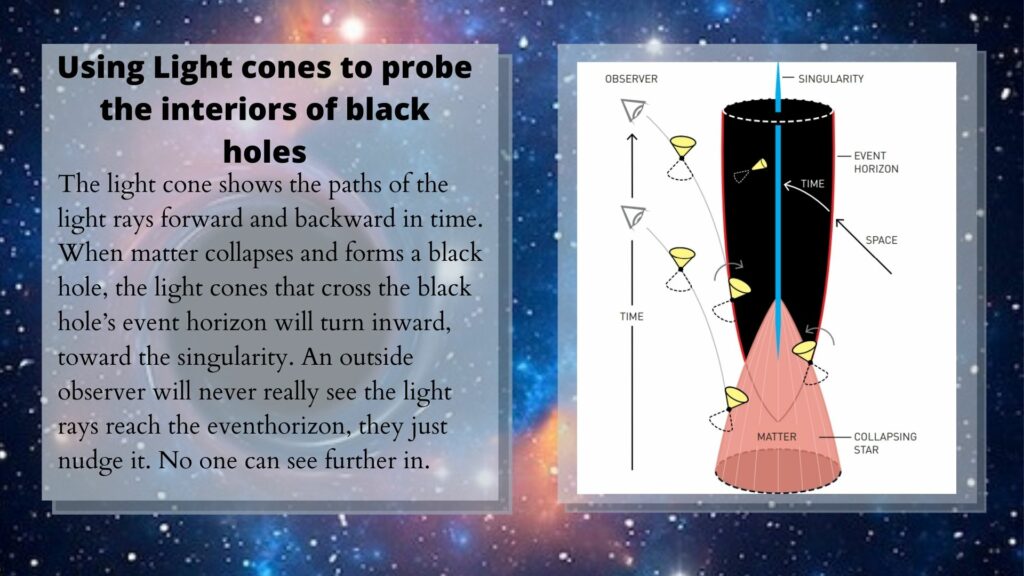
However, towards the static limit — the point at which the black hole starts to drag spacetime around with it — the lightcones begin to tip towards the singularity and in the direction of rotation and narrow. Thus the static limit represents the point at which light is no longer free to travel in any direction. It must move in a direction that doesn’t oppose the rotation of the black hole. Particles at this limit can no longer sit still — hence the name static limit.
Yet, despite the fact the dragging effect is so strong, here that not even light can resist it, signals can escape this region — it isn’t the event horizon — but they can only do so by travelling in the direction of the rotation.
Interestingly, Penrose suggests that particles entering the static limit and decaying to two separate particles may result in energy leaching from the black hole in what is known as the Penrose process, but that’s a discussion for another time.
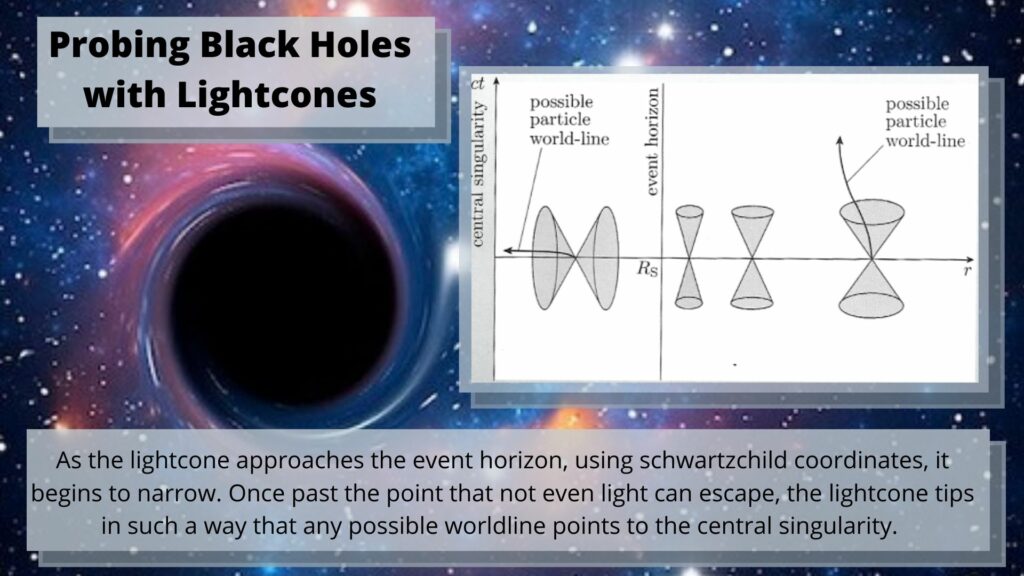
So as our light cone moves toward the event horizon, it begins to narrow and tip. But, something extraordinary happens when it passes this boundary. As long as one is using so-called Swartzchild coordinates, once ‘inside the black hole’ proper, the lightcone flips on its side, with the ‘future end’ of the cone pointed towards the singularity.
This can mean only one thing for the worldline of that event, it points to the central singularity signalling that an encounter with that singularity is evitable.
The Anatomy of a Black Hole
“It is generally believed that the spacetime singularities of gravitational collapse will necessarily always lie within an event horizon, to that whatever happens to be the extraordinary physical effects at such a singularity, these will be hidden from the view of any external observer.”
Roger Penrose, The Road to Reality
Black holes aren’t particularly complex in construction and posses only three properties –mass, electric charge, and angular momentum–but physicists working with light cones were able to determine the layers of their anatomy–and crucially, the bounded surfaces that exist within them.
This is what was revolutionary about Penrose’s concepts, they introduced the concept of bounded surfaces to black holes.
Looking back on this from an era in which a black hole has been imaged for the first time and gravitational waves are beginning to be routinely measured from the mergers of such objects, it’s important to not underestimate the importance of Penrose’s findings.
Before any practical developments surround black holes could even be dreamed of, Roger Penrose provided the mathematical basis to not just suggest the existence of black holes, but also laying the groundwork for their anatomy, and the effect they have on their immediate environment.
Thus, what Penrose’s Nobel award can really be seen as a recognition of moving these objects — or more accurately, spacetime events — from the realm of speculation to scientific theory.

Original research and further reading
Penrose. R., ‘Gravitational Collapse and Space-Time Singularities,’ Physical Review Letters, vol. 14, Issue 3, pp. 57-59, [1965]
Penrose. R., ‘The Road to Reality,’ Random House, 2004
Senovilla. J. M. M., Garfinkle. G., ‘The 1965 Penrose Singularity Theorem,’ Classical and Quantum Gravity, [2015].
Relativity, Gravitation and Cosmology, Robert J. Lambourne, Cambridge Press, 2010.
Relativity, Gravitation and Cosmology: A basic introduction, Ta-Pei Cheng, Oxford University Press, 2005.
Extreme Environment Astrophysics, Ulrich Kolb, Cambridge Press, 2010.
Stellar Evolution and Nucleosynthesis, Sean G. Ryan, Andrew J. Norton, Cambridge Press, 2010.
Cosmology, Matts Roos, Wiley Publishing, 2003.
Was this helpful?



