Prime numbers are like the special beasts of the mathematical world. Just like how some animals are one-of-a-kind, prime numbers are truly unique: they can’t be divided by any number other than 1 and themselves.
Think of it this way: if you take any prime number and you look for any number that divides it, you’ll never find anything else other than 1 and itself; but if you take any other number, you’ll always find at least an another one. If you take the number 10, for instance, it’s divided by 1, 2, 5, and 10; if you take the number 27, it’s divided by 1, 3, 9, and 27. But if you take numbers like 7, 11, 29, or 97, it’s only 1 and themselves.
But there’s even more to prime numbers than that.
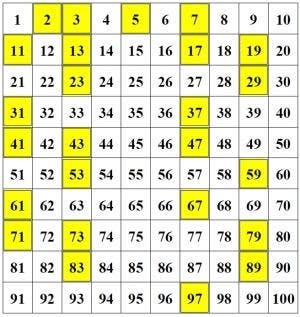
A prime number must satisfy three conditions:
- it must be a natural number (so numbers like 1.2, -7, or √3 are out of the question);
- it must be greater than 1;
- it must not be the product of any two other numbers.
So essentially, a prime number is any natural number starting from 2 that isn’t divisible by any numbers other than 1 or itself. Let’s take a few more examples:
- 5 is a prime number, it can only be written as a product of 1 x 5;
- 6 is not a prime number, it can be written as 2×3.
Prime numbers extend indefinitely, but computing them becomes more and more challenging. The largest prime number we know of is 282,589,933 − 1, a number so great that it has 24,862,048 digits. Yeah, let’s not write that down.
But computing smaller prime numbers, and analyzing whether a number is prime, isn’t all that challenging.
A number that is not prime is called composite. All natural numbers are either primes or composites.
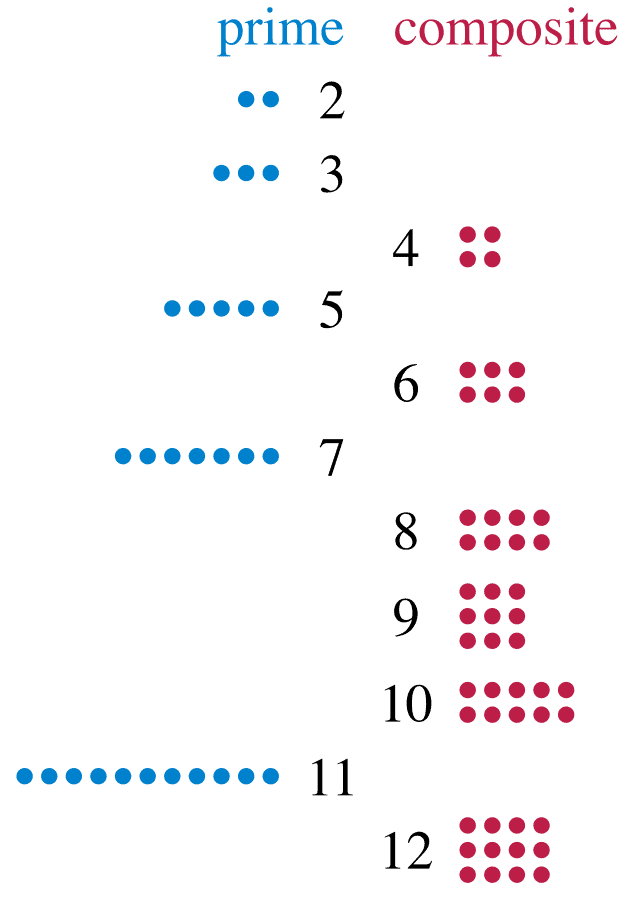
The basics of prime numbers
All natural numbers are either primes or composites — but what does that really mean? Well, it basically means that if we take any natural number, it can be either written as a product of two other numbers, or it’s a prime. There’s no middle way. If we look at the image above, 12 is written as 4 x 3. It can also be written as 6 x 2, but it doesn’t matter.
Whether there’s one way to write a number as a product or a million ways to write it as a product, it’s still a composite number, and therefore not prime.
If prime numbers are unique beasts of the mathematical world, composite numbers are more common animals.
Checking if a number is a prime
Every prime number can only be written as ‘1’ times itself. Every composite number can be written as a product of prime numbers (something called prime factorization).
The rough way to search for prime numbers is to start incrementing and check if any numbers divide it evenly. In other words, if it has any divisors other than 1 and itself, it’s not prime. It’s time consuming, but it gets the job done.
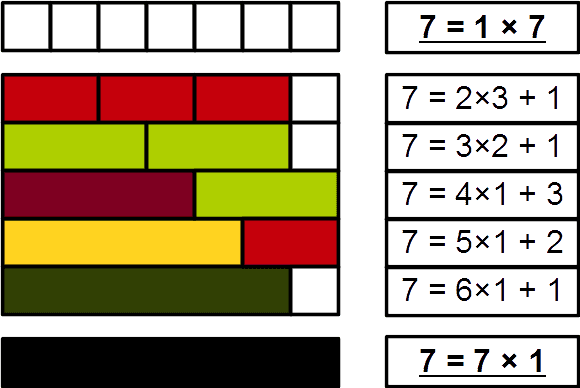
But we can get a bit more clever and efficient about our search for prime numbers.
We can weed out half of them right from the start. How? By using the number ‘2’. Every number is either odd or even, by definition. Even numbers are divisible by 2, which means they can be written as 2 times something — and are therefore composite, not prime. The number ‘2’ is the only even prime number.
If you’re trying to see whether a number is prime, and it doesn’t divide by 2, it’s not going to divide by 4, 6, 8, 10… either. Then, you can use the same approach: find prime numbers and used them to weed out other numbers.
For instance, ‘3’ is a prime number, so it can be used to weed out other numbers that aren’t prime. If a number doesn’t divide by 3, it’s also not going to divide by 6, 9, 12… — and if a number doesn’t divide by 5, it’s also not going to divide by 10, 15, 20… and so on.
This is actually a very old algorithm used to discover prime numbers: you start from 2, and then for every prime number you encounter, you use it to weed out its multiples. You don’t need to use ‘4’ since it is an even number, and we already know that other than ‘2’, no prime number is even. So we can just move on to 5, 7, and move on.
This is called a ‘sieve’, and commonly, the ‘sieve of Eratosthenes’, since the ancient Greek mathematician Eratosthenes first described it. You can see a visual representation of how it works in the image below:
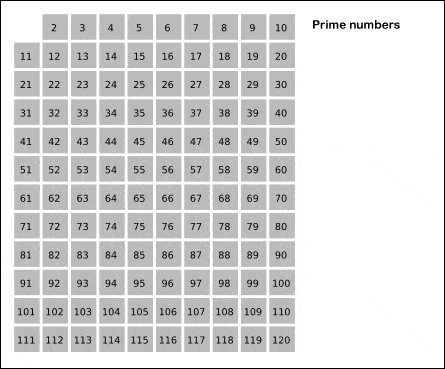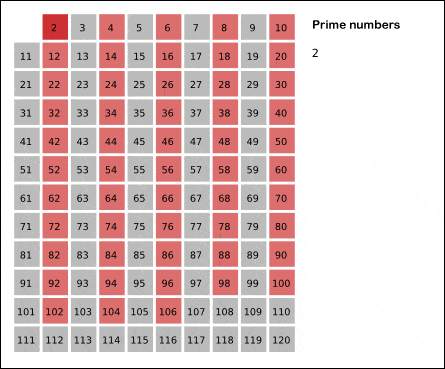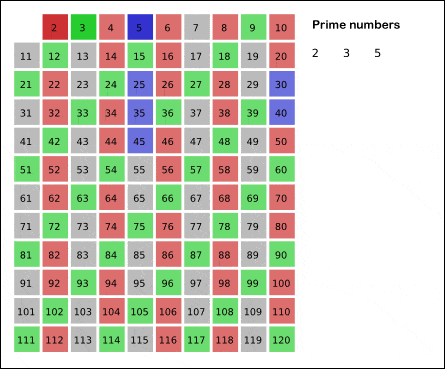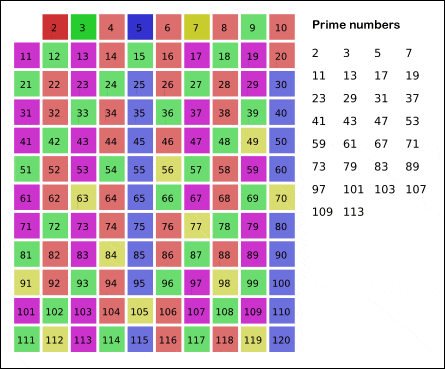
You can even more clever with your prime-finding sieves. For instance, let’s say you want to check if the number 100 is prime (spoiler alert, it’s not). You don’t need to check every number from 2 to 100, you can stop with your checks at 50, which is half of 100. Why? Look at it this way:
- every number can be written as: number (n) = ‘half’ x 2. Every number is twice its half, basically. If you reach a number beyond its half and you haven’t found anything that divides it, you’re not going to find anything after its half either.
We upgrade our algorithm one more time: you don’t even need to check until half of the number, you only need to check to its square root (√n) — but we won’t go into demonstrating this just yet.
| 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | |
| 29 | 31 | 37 | 41 | 43 | 47 | 53 | 59 | 61 | 67 |
| 71 | 73 | 79 | 83 | 89 | 97 | 101 | 103 | 107 | 109 |
| 113 | 127 | 131 | 137 | 139 | 149 | 151 | 157 | 163 | 167 |
| 173 | 179 | 181 | 191 | 193 | 197 | 199 | 211 | 223 | 227 |
| 229 | 233 | 239 | 241 | 251 | 257 | 263 | 269 | 271 | 277 |
| 281 | 283 | 293 | 307 | 311 | 313 | 317 | 331 | 337 | 347 |
| 349 | 353 | 359 | 367 | 373 | 379 | 383 | 389 | 397 | 401 |
| 409 | 419 | 421 | 431 | 433 | 439 | 443 | 449 | 457 | 461 |
| 463 | 467 | 479 | 487 | 491 | 499 | 503 | 509 | 521 | 523 |
| 541 | 547 | 557 | 563 | 569 | 571 | 577 | 587 | 593 | 599 |
| 601 | 607 | 613 | 617 | 619 | 631 | 641 | 643 | 647 | 653 |
| 659 | 661 | 673 | 677 | 683 | 691 | 701 | 709 | 719 | 727 |
| 733 | 739 | 743 | 751 | 757 | 761 | 769 | 773 | 787 | 797 |
| 809 | 811 | 821 | 823 | 827 | 829 | 839 | 853 | 857 | 859 |
| 863 | 877 | 881 | 883 | 887 | 907 | 911 | 919 | 929 | 937 |
| 941 | 947 | 953 | 967 | 971 | 977 | 983 | 991 | 997 |
Just like how we protect and preserve rare and unique animals, prime numbers play a big role in many areas of mathematics and science, and scientists cherish them. Looking for prime numbers is a common exercise not just in mathematics, but also in programming, where the goal is learning how to devise and optimize an algorithm. Prime numbers also play a key role in security.
A list of prime numbers up to one thousand:
Some properties of prime numbers
Prime numbers may seem like just a new quirk, but mathematicians have been fascinated with them for millennia (as we’ll see in a bit). They have several properties that make them special — here are just a few of them.
- There are infinite prime numbers
The sequence of prime numbers never ends. It can get harder and harder to find prime numbers, but there will always be an even larger one. This was first proven by the Ancient Greek mathematician Euclid. The longest prime number we know of is 22 million digits long.
- There is no super-efficient formula for calculating prime numbers
Sure, we’ve found a few ways to make our quest for prime numbers more efficient, but mathematicians have been looking for better tools for a long time, and haven’t really found a clear rule that can explain the distribution of prime numbers. This is one of the things that makes prime numbers so attractive. We don’t know when and how prime numbers occur, we can just calculate them.
- 1 is not technically a prime number
This sometimes starts weird debates and is not truly consequential, but 1 is not typically considered a prime number. There’s no strict reason for that, however. Ancient Greeks (and Arabic mathematicians as well) did not consider 1 to be a number in the sense that all other numbers are — it was more a unit for numbers than a number itself. In the 18th and 19th centuries, some mathematicians considered it prime, while others did not. Nowadays, we don’t really consider it a prime, if only for the fact that we would have to rewrite the definition of prime numbers in a way that’s more awkward.
- Numbers can be prime among themselves (but not technically primes)
Two numbers that don’t have any common divisors are considered to be ‘coprime’ — and this doesn’t really mean that they are really primes (though they can be). For instance, the numbers 25 and 4 are coprimes, because 25=5×5, while 4=2×2, and they have common divisors.
History of prime numbers

You may think that prime numbers are a modern quirk that mathematicians came up with, but they’ve actually fascinated people for centuries — nay, millennia. An Egyptian papyrus dating from 3,550 years ago references prime numbers, and Euclid’s landmark Elements work demonstrates that there are infinitely many prime numbers. Several well-known Greek mathematicians dealt with prime numbers, including Eratosthenes, whose sieve we’ve just looked at.
Coincidentally or not, the period in which people didn’t seem really interested in prime numbers is a period we now call the Dark Ages. Some Islamic mathematicians looked at prime numbers, which Fibonacci brought to Europe, translating and analyzing the work. After that, most brilliant mathematicians looked at prime numbers: Pierre de Fermat stated (but did not prove) Fermat’s little theorem, which was later proved by Leibniz and Euler.
Many mathematicians have also tried to find ways to predict the emergence of prime numbers, but this has proven a hidden Graal. Since 1951, all the largest known prime numbers have been discovered using computers.
Why prime numbers matter so much
For a very long time, prime numbers were canonical and pure — a quirk of mathematics, but with little significance outside of mathematics. Now, we know this to be untrue and prime numbers have important applications in several fields.

For instance, the number of cogs on two gears is often chosen to prime among themselves, to create an even contact between every cog of both wheels and avoid unnecessary wear and damage — but this is not technically an application of prime numbers.
The first moment when primes became really important was in the 1970s when it was first announced that prime numbers could serve as the basis of public-key cryptography algorithms. In other words, every time you use the internet to send an encrypted message (like you probably do daily), it uses an algorithm based on prime numbers, specifically because they’re so mysterious and hard to assess.
Prime numbers also play a part in fields such as quantum mechanics and abstract algebra. Perhaps even more intriguing, prime numbers have been shown to also play a role in some biological species. The cicadas of the genus Magicicada, for instance, spend most of their time as grubs beneath the ground. They emerge after 7, 13, or 17 years — all prime numbers. This is not a coincidence, biologists believe: cicadas emerge in this fashion to prevent predators from synchronizing with their lifecycle. In addition to the many applications of prime numbers in mathematics, modern research seems to indicate that at least in some cases, prime numbers also play a role in other fields.
Prime number research is far from over. Undoubtedly, there are many more prime mysteries waiting to be uncovered — this is only scratching the surface.
Was this helpful?