
Quantum computers promise to power humanity into a new computing revolution, not all that different in magnitude as the jump from office-sized vacuum tube computers to the miniaturized CPUs packed with millions of tiny transistors we all know and love today. Since the early 2000s, quantum computing has been all the rage among computer science scholars for very good reasons. Now, the fruits of their labor are beginning to show.
Now we can come out and play
For the first time, a team of researchers claims it’s made a fully programmable and reconfigurable quantum computer module. This module can easily be configured to run various algorithms without having its hardware specifically designed for that sole use, and that use only. Basically, we’re finally getting to see tangible results with quantum computing, something that the general public might actually get to use in the coming decade — a quantum computer that might one day be as versatile as our laptops and smartphones.
“For any computer to be useful, the user should not be required to know what’s inside,” said Christopher Monroe, a Fellow of the Joint Quantum Institute and the Joint Center for Quantum Information and Computer Science.
“Very few people care what their iPhone is actually doing at the physical level. Our experiment brings high-quality quantum bits up to a higher level of functionality by allowing them to be programmed and reconfigured in software.”

Programmable and reconfigurable are definitely keywords here, but first a few words on quantum computers, to understand how quantum computers are different from classical ones. Basically, a classical or conventional computer handles operations in the same way that people compute by hand — one at a time, sequentially. Yes, an eight-core processor is a heck of a lot faster at adding numbers than me or you, but still far from perfect. What quantum computers promise is solving operations in parallel, drastically upping speed. Some tasks like modeling the climate or astronomical events can literally take hundreds of years for the fastest supercomputers on the planet to solve, but only minutes for a big enough quantum computer.
Fundamentally, a quantum computer can achieve this by working with qubits or quantum bits, instead of digital bits. A conventional computer stores information in bits which can either be 0 or 1, but a qubit can be in states labeled 0 or 1, but it can also be in a superposition of these states, a|0} + b|1}, where a and b are complex numbers. In other words 0 and 1 at the same time, a weirdness whose explanation is beyond the scope of this article for now. For every extra qubit you get, you can store twice as many numbers. For example, with 3 qubits, you get coefficients for |000}, |001}, |010}, |011}, |100}, |101}, |110} and |111}.
The reprogrammable quantum module made by researchers at the Joint Center for Quantum Information and Computer Science at the University of Maryland has five qubits, meaning it can store 32 numbers at the same time. But that’s not what’s impressive about it — other teams demonstrated machines with far more qubits.
What’s remarkable is that these qubits are stored in atomic ions which are shielded by fields from nearby electrons. The ions stay trapped and can be manipulated if the situation requires it using tightly-focused laser beams, and by measuring the glow of each ion scientists could determine the state of the qubit. Most importantly, this setup is built as a module, meaning more such devices can be stacked to scale the number of qubits — up to one hundred.
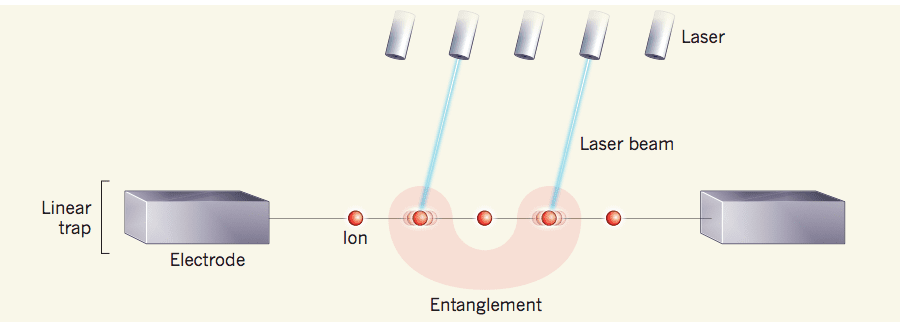
“By directly connecting any pair of qubits, we can reconfigure the system to implement any algorithm,” said Shantanu Debnath, the paper‘s lead author, in a statement.
“While it’s just five qubits, we know how to apply the same technique to much larger collections.”
To test the module, not one but three algorithms were run, including a demonstration of a Quantum Fourier Transform (QFT), which finds how often a given mathematical function repeats. This is where it gets very interesting as far as ‘real life’ applications go. All your banking transactions, online accounts or virtually anything that’s encrypted relies on the RSA algorithm, first introduced in 1977.
Using this asymmetric cryptography (RSA), two different but mathematically linked keys, one public and one private, are used to decrypt a message. The public key, which anyone can see and use to encrypt a message, is based on the product of two large primes, and an auxiliary exponential. Multiplying two large primes to an integer is easy, but determining the original primes that make the product with no other info is very difficult.

In 1994, Peter Shor, the Morss Professor of Applied Mathematics at MIT, came up with a quantum algorithm that calculates the prime factors of a large number, vastly more efficiently than a classical computer. To actually run the algorithm though a quantum computer would require many qubits or quantum bits. If you have enough, though, RSA encryption will instantly become obsolete. The Quantum Fourier Transform (QFT), which the University of Maryland computer scientists ran on their module, is a key component of Shor’s algorithm. Two of the algorithms ran successfully more than 90% of the time, while the QFT topped out at a 70% success rate.
“By reducing an algorithm into a series of laser pulses that push on the appropriate ions, we can reconfigure the wiring between these qubits from the outside,” Debnath offers in a statement. “It becomes a software problem, and no other quantum computing architecture has this flexibility.”

Was this helpful?